Биномно и геометрично разпределение - схеми на Бернули
Да предположим, че хвърляме несиметрична монета с вероятност за “ези” , равна на p и за “тура” - равна на q.
Тези две страни на монетата се наричат съответно "успех" и "неуспех".
p+q = 1
Тура ( от турски ) се нарича една от страните на монетата, на която е изобразен печатът или
калиграфският подпис на султана.
Думата “ези” е от персийското “евза” , което означава лице.
Ако търсим вероятността за k успеха в общо n опита трябва да имаме предвид, че опитите са независими и
успехите могат да бъдат раположени на k места от общо n.
Тази вероятност е равна на
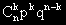Тя се означава с b( k,n,p ) и се нарича бернулиева.
Ще пресметнем нейната средна стойност.
Заместваме p с x и диференцираме спрямо x.
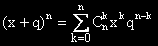
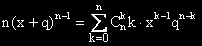
Умножаваме по x и накрая, обратно заместваме x с p.
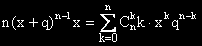
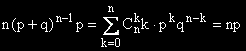Понеже p+q = 1.
|
Средната стойност на Бернулиево разпределена случайна величина е np.
|
Схема от последователно повтарящи се опити с два изхода с постоянна вероятност се нарича „Схема на Бернули”.
Такава е схемата, състояща се от последователното подхвърляне на монета, като се отчита събитието
“Брой неуспехи до първия успех”.
Този брой може да бъде нула, ако от първия път се падне „успех”.
Едно е ако при второто хвърляне се падне „успех” а първото е „неуспех” и т.н.
Вероятността за n последователни неуспеха, последвани от успех е qn.p ( n=0, 1, 2, ...) .
Това разпределение се нарича „геометрично”.