По страницата се работи!
Какво трябва да знаем:     Елементи от комбинаториката  
Условна вероятност – независими събития 		Теория на вероятностите
Висша математика III част

Сметало за комбинаторика и схемата на Бернули

Функции и указания за работа

n - факториел 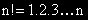n - факториел -Fact1       По дефиниция 0! = 1.
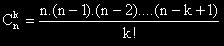
Биномни коефициенти или комбинации от n елемента k-ти клас. Биномни коефициенти -C_k_n0
Под термина „схема на Бернули” се разбира повтарянето на един опит с два възможни изхода – „успех” и „неуспех”.
Вероятността за “успех” е p а за “неуспех” - q като p+q=1. Отделните събития – “успех” или “неуспех” се считат за независими.     Опитът се повтаря n пъти.     Броят на успехите при тези n повторения ще означа с Sn.
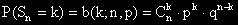
Вероятността при тези n повторения на опита да се получат k „успеха” се означава с b(k; n, p). и е равна на Вероятността за k успеха -P1
Броят на успехите с най-голяма вероятност се нарича мода и при биномното разпределение се означава с M(n,p) и е равен на най-близкото цяло число до (n+1).p. Означава се с [(n+1).p].
Вероятността да се получат r или повече успехи е 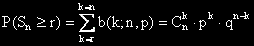Вероятността за повече от r на брой успехи -P2 Тази вероятност ще означаваме с B(r; n, p).

Ако n е твърде голямо число а p - твърде малко така, че произведението λ = np е едно обозримо за нашите пресмятания число беномното разпределение може да се замени с експоненциално с параметър λ .

Предложеното сметало пресмята дефинираните функции. В него има най-много три входни аргумента, означени над входящите полета.
При някои от функциите се вземат предвид само един или два от тях а останалите са без значение.

Дано сметалото Ви донесе полза, знание и радост.
Очакваме критики.

Сметало за комбинаторика и за схемата на Бернули

k n p
Какво ще научим:    
Сметало за разпределението на Поасон
Поасоново разпределение 		Теория на вероятностите
Висша математика III част