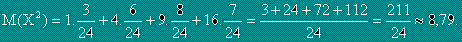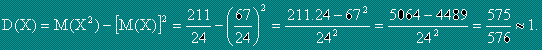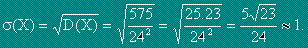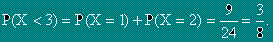Числови характеристики на дискретна случайна величина -
математическо очакване и дисперсия

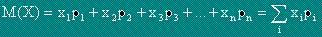
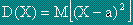
Математическо очакване M(X) (или средна стойност) на дискретна случайна величина X се нарича сумата от произведенията на всички възможни стойности на случайната величина по съответните им вероятности. Дисперсия D(X) ( разсейване ) на случайната величина X се нарича математическото очакване на квадрата на отклоненията на случайната величина от нейното математическо очакване. 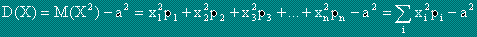където a=M(X) Доказва се, че Стандартно отклонение s(X) се нарича корен квадратен от дисперсията.

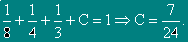
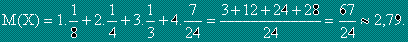
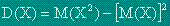Сумата от вероятностите трябва да е 1. Таблицата на разпределение придобива вида: Стойност на сл.вел X 1 2 3 4 Вероятност P(X) 1/8 1/4 1/3 7/24 Пресмятаме За M(X2): Стойност на сл.вел X2 1 4 9 16 Стойност на сл.вел X 1 2 3 4 Вероятност P(X) 3/24 6/24 8/24 7/24 или 8,79-(2,79)2 със същия резултат.