Случайни величини

Какво трябва да знаем:
Случайни събития и действия с тях
Вероятност на случайно събитие

Съдържание на висша математика I част
Съдържание на висша математика II част
Съдържание на висша математика III част

Случайни величини

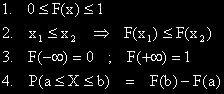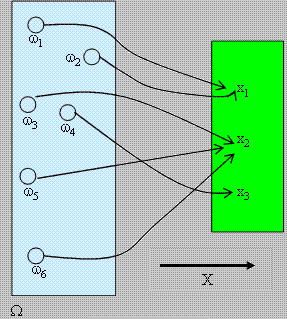
Случайна величина се нарича числова величина,
появяваща се в резултат на опит със случаен изход.

Случайните величини се означават с големи латински букви X, Y …, а приеманите от тях стойности – със съответните малки: x₁ , x₂ , ... , y₁ , y₂ , ....
Случайната величина е числова функция, определена в пространството W на елементарните събития.

По такъв начин на всяко елементарно събитие w от W се съпоставя число – X(w).
За да се получи пълна представа за случайната величина, не е достатъчно да се знае само съответствието, съпоставящо на всяко елементарно събитие съответната му стойност.
Трябва да се знае и вероятността за получаване на тази стойност.

Всяко правило, позволяващо да се намери вероятността на събитието
случайната величина да заеме определена стойност или
да попадне в даден интервал се нарича
закон на разпределението на случайната величина.

Пример 1.
Хвърля се зар.
Отчитат се точките.
Случайната величина е със стойности от 1 до 6.
Всяка от тях се получава с вероятност 1/6.
Законът на разпределение може да се зададе таблично:

X	1	2	3	4	5	6
P(X)	1/6	1/6	1/6	1/6	1/6	1/6

Пример 2.
В град с население S = 30 456 се избира един жител.
Случайната величина X е неговия доход.
Стойността на X може да е произволно, неотрицателна число.
Ние можем да въведем разумно ограничение, ако в този град не живее г-жа Мургина, но това не променя нещата, защото между числата 200 и 201, например, има безбройно много числа.
Затова приемаме, че разлика от 100 лева за нас е несъществена.
Тогава населението може да бъде разделено на групи.
В I група попадат жители с доход до 100, във II - от 100 до 200, в III от 200 до 300 и т.н. до последната – с доходи над 1000.
Ако в първата група попадат n₁ на брой жители, то вероятността, произволен жител да попадне в нея е p₁ = n₁ / S.
Аналогично можем да определим и вероятностите за останалите групи.
Така можем да дадем табличния закон на разпределение при направените разумни ограничения.

X	до 100	над 100 под 200	над 200 под 300	над 300 под 400	...	...
P(X)	p₁	p₂	p₃	p₄	...	...

Функция на разпределение на случайната величина X се нарича функцията F_X( x ) = P( X < x ) –
вероятността за това, случайната величина да заеме стойност по-малка от x.

Функция на разпределение притежава следните свойства:

За първия пример F(1) е вероятността показанието на зара да е по-малко от 1, която е 0.
Следователно F(1) = 0.
F(4) е вероятността да се падне 1, 2 или 3, която е 1/6 + 1/6 + 1/6 = 1/2 .
Следователно F(4) = 0.
Толкова е и F(3,5), защото не може да се падне нищо по-голямо от три и по-малко от три и половина.

Какво ще научим:
Дискретни случайни величини (работим)