Ако четем – пишем. Ако не пишем – не четем. Ако пишем – мислим.
Какво трябва да знаем:    
Умножаване на матрици   Преход от полярна координатна система в декартова и обратно  
Якобиан - преход от едни координати към други в равнината   Частни производни    
Производна на сложна функция на повече променливи
Диференциална геометрия
Висша математика II част
Векторен анализ

Якобиани и действия с тях

Нека f е функция на промеливите ( x 1 , x 2 , x 3 , ... x n ).       ( Горните индекси не са степени! )
Чрез символа Ред, състоящ се от частните производни Jacobian1Xn_1 ще означаваме вектор-реда, Vect1 ,
състоящ се от частните производни на f спрямо променливите x i .

Нека Преход от декартови в полярни координати Sys_xy        Ще намерим x_rPhi и y_rPhi .
Ex1_1

Нека x = x( r, ψ , φ ) = r.sinψ.cosφ .         Ex2_0 =
Ex2_1


Нека f и g са функции на промеливите ( x 1 , x 2 , x 3 , ... x n ) . Под символа fg_xi се разбира матрица, състояща се от два реда и n стълба.       Първият ред е Ред, състоящ се от частните производни на f Jacobian1Xn_1 а вторият – Ред, състоящ се от частните производни на g Jacobian_g
Нека Преход от декартови в полярни координати Sys_xy .       _xy_rPhi =
Ex3_1

Нека xy_rPsiPhi       Ex4_0 =
Ex4_1

Изобщо, ако y1 , y2 , y3 ,..., ym са функции на x1 , x2 , x3 ,..., xn то ym_xn е матрица, състояща се от m реда и n стълба. Нейният i – ти ред и j – ти стълб е частната производна Dxi_Dyj
Ако говорим за смяна на координатната система то m = n. Горните променливи се наричат „стари” координати а долните „нови”.
В този случай, матрицата или нейната детермнанта се нарича якобиан. Така ще наричаме и матрицата в общия случай – при m ≠ n.
Например, преходът от от декартови към полярни координати се извършва по формулите: Преход от декартови в полярни координати Sys_xy , макар че е странно, понеже трябва да знаем ( r, φ ) – “новите” координати за да намерим “старите” – ( x, y).
Наименованията „нови, стари” идват по-скоро от това, че якобианът _xy_rPhi
се явява матрица на прехода от стария базис - (i, j) към новия (r, φ ).
_3Draw

Вярно ле е, че Ex5_0 ?       ( Прилича на съкращаване! )
Тук f(x, y). От своя страна x и y са функции на u.
Така, че f се явява функция на u, но опосредствено от x и y.
f = f(x, y) = f(x(u), y(u)) = f(u).
От формулата за производна на сложна футкция на повече променливи получаваме: Ex5_1 .
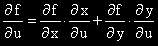
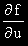
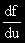
Пишем „криви дета” за Ex5_2 , макар че е по-правилно Ex5_3 от съображение за „благописане”.
Последното равенство в матричен вид изглежда така: Ex5_4

Изобщо Ex6_0
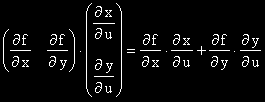
Умножаваме r - тият ред на първия множител по s – тия стълб на втория.
Ex6_1

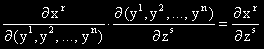
Това е (r, s) - тият елемент на матрицата отдясно. ( Номерът на реда е отгоре а на стълба – отдолу. )

Тогава: Ex6_2, където En е единичната матрица от n–ти ред.
Например да разгледаме преходът от декартова координатна система в полярна и обратно.
Първият преход се извършва по формулите за преобразуване: Преход от декартови в полярни координати Sys_xy
Обратният преход се извършва като изразим новите координати (r, Φ ) чрез старите (x, y). Right_Inv
Ще проверим равенството Ex7_0
Ex7_1
_3JacobCalc
Ex7_2

Трябва да докажем, че двете матрици са обратни. Да изразим елементите на последната чрез (r, φ).
Ex7_3

Чрез непосредствено умножаване се уверяваме във верността на твърдението.


Какво ще научим:        Сферични координати - якобиан       Цилиндрични координати