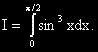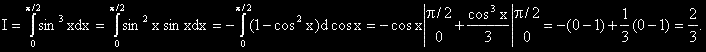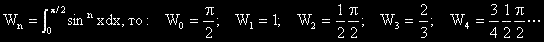Какво трябва да знаем:
Неопределени интеграли - дефиниция
Основни елементарни функции и техните графики
Внасяне под знака на диференциала и сложен интеграл
Съдържание на висша математика I част

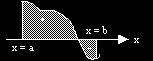
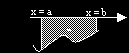
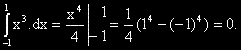
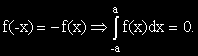
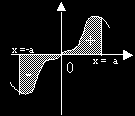
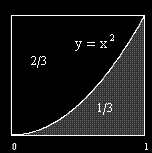
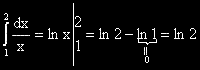
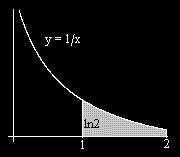
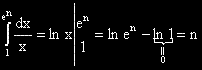
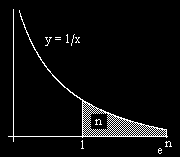
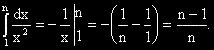
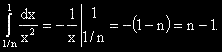
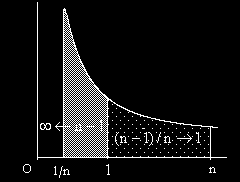
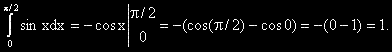
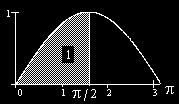
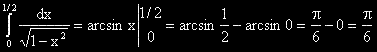
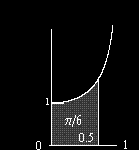
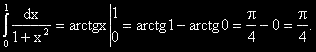
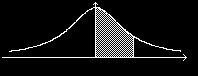
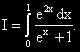
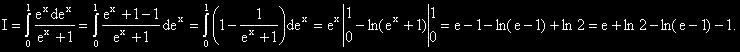
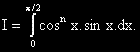
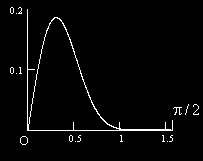
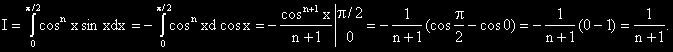
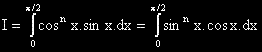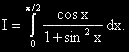
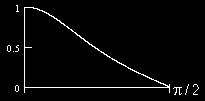
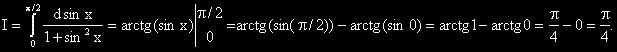
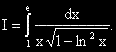
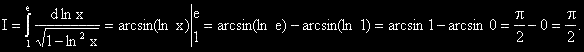
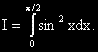
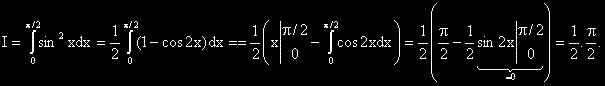
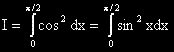Определен интеграл - въведение



Тази формула, както вече знаем се нарича формула на Нютон-Лайбниц.
Геометричният смисъл на определения интеграл е лицето на фигурата между двете вертикални прави: x = a и x = b, абцисата и графиката на функцията y = f(x).
Ако графиката е над абцисната ос, това лице се отчита със положителен знак а ако е под – с отрицателен.

При пресмятане на определения интеграл е желателно да скицираме графиката на подинтегралната функция в интервала [a;b].

Изобщо, интеграл от нечетна функция, в симетрична спрямо нулата област, е равен на нула.
Ако f(x) e нечетна:


Ако f(x) e четна:

Това равенство показва, че лицето на криволинейния триъгълник, заграден от графиката на функцията y = x2,
абцисата и вертикалната права x = 1 e 1/3.


     

     

Това е площта, защрихована отдясно на вертикалната права x = 1.
При n клонящо към безкрайност тази площ клони към 1.
Получава се една площ, която има безкрайна обиколка, но крайно лице.
Ако разгледаме интеграла в граници [1/n; 1], получаваме, на пръв поглед парадоксалния резултат:

Така, че защрихованата площ отляво на 1 клони към безкрайност.

Странни работи се явяват в математиката!

Известният формализъм за внасяне под знака на диференциала може свободно да се използва и тук.

Подинтегралната функция е положителна в [0;1], така че очакваме положителен резултат.

На чертежа е изобразена графиката на y = cos10 x.sinx.
Вярно ли е че:           ?
И ако "да", или "не", или "не може да се каже", питам аз "Защо?" и отговор не искам.
     

По един чуден начин в горната задача, сякаш че от шапката на фокусника, сред логаритми и корени се появява числото p.
Но има нещо още по-странно: при x = e подинтегралната функция не е дефинирана.
Може ли така?
И ако "да", или "не", или "не може да се каже", питам аз "Защо?" и отговор не искам.
Защото и аз не мога да кажа.


Вярно ли е че: ?
Нека да се напънем и да пресметнем интеграла:


Ако означим:
Можете ли да продължите тази редица?
Ако проявавате нездрав интерес към тези равенства, насочете се към формулите на Уолис, но преди това трябва да усвоите интегрирането по части в определения интеграл.


Какво ще научим:
Интегриране по части при определения интеграл
Формули на Уолис
Полагания при определен интеграл