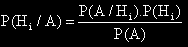
Формула на Бейс
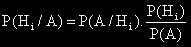
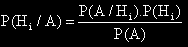
Формула на Бейс
Вероятностите P( H i ) се наричат "преди опитни" или "априарни".
След появяването на събитието A те трябва да бъдат заменени с P(H i / A ).
Тези вероятности се наричат "след опитни" или "апостериорни".
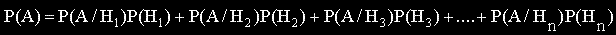 ,
,
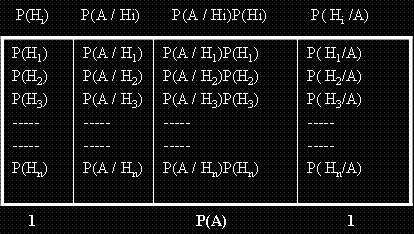
|
Пример 1 В две еднакви урни са поставени бели и черни топки. В първата има 3 бели и 4 черни а във втората 2 бели и 3 черни. Каква е вероятността да извадим бяла топка ( събитие A ), от случайно избрана урна? Ако е изветно, че сме извадили бяла топка, каква е вероятността да сме я извадили от първата и каква от втората урна? |
|
Пример 2 В една урна има две топки – бяла и черна а в друга – 2 бели и 3 черни. От първата изваждаме една топка и без да я поглеждаме я поставяме във втората. След това от нея изваждаме втора топка. Каква е вероятността тя да е бяла ( събитие A )? Ако се е сбъднало събитието A, намерете вероятността първата топка да е била бяла и вероятността тя да е била черна. |
|
Пример 3 Техническо устройство ще откаже ако са неизправни не по-малко от 2, от трите независимо работещи елемента. Вероятността за техния отказ е съответно 0,2 ; 0,4 и 0,3. Известно е, че устройството не работи ( събитие A ). Намерете вероятностите за неизправност на първия, втория и третия елементи. |