Какво трябва да знаем:
Събития и действия с тях – хипотези
Вероятност на случайно събитие
Условна вероятност
Съдържание на висша математика I част
Съдържание на висша математика II част
Съдържание на висша математика III част

Формула на пълната вероятност


Ако H1 , H2 , H3 , …. Hn са хипотези и A е случайно събитие то
Понеже A е сума на несъвместими събития,
вероятността на събитието A е сума от вероятностите на събираемите.


От формулата за умножаване на вероятностите следва:
Така получаваме:


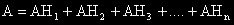
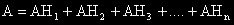
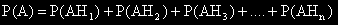
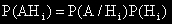
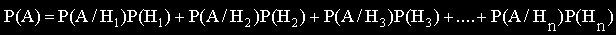
"Формула за пълната вероятност"

В задачите, обикновено се описват хипотезите Hi ,
задават се техните вероятности и
условните вероятности P(A / Hi ).
Добре е данните да се подредят в таблица.


Сумата от вероятностите на хипотезите, разположени в първата колона трябва да е 1.
Вероятността на A е сумата от вероятностите, разположени в третата колона.



Пример 1
45% от телевизорите в един магазин са произведени от I завод, 15% от II а останалите от III.
Вероятностите за това, телевизорите произведени от тези заводи да не изискват ремонт в продължение на гаранционния срок са съответно 0,96 , 0,84 , 0,90.
Намерете вероятността, случайно купен телевизор да работи безотказно в течение на гаранционния срок.




Пример 2
С цел повишаване на надежността на съобщенията се използва дублиране на комуникационната система.
Вероятността за прием на сигнала от всяко от двете устройства е 0,8 а тази, за предаване на полученото след приема съобщение 0,9.
Каква е вероятността за предаване на полученото съобщение от дублираното устройство?




Пример 3
Имаме три кутии, в една от които има награда.
Състезател избира една от тях без да я отваря.
Съдята отваря една от останалите две кутии, която се оказва празна.
Той предлага на състезателя или да запази избраната от него кутия, или да избере друата – единствено останала.
Кой от двата варианта е по-изгоден са състезателя?



Какво ще научим:
Формула на Бейс