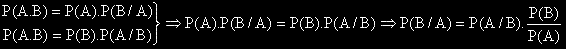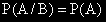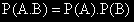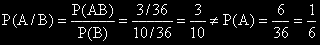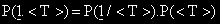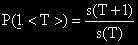Условна вероятност
Нека A и B са събития.
Условна вероятност на A при условие B (означава се с P(A/B) )е вероятността на A,
намерена при условие , че събитието B се е сбъднало.
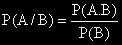
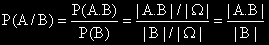
Теорема (правило за умножение на вероятности)
Вероятността на произведение на две събития е равна на произведението на вероятността на едното по условната вероятност на другото, при условие, че първото се е сбъднало.
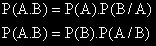
Ако знаем P(A) , P(B) и P(A/B) , можем да намерим P(B /A) по формулата:
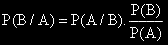 , защото:
, защото:
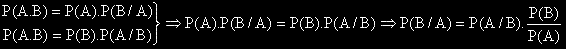
Събитието A се нарича независимо от събитието B, ако вероятността на A не зависи от това,
дали се е случило или не събитието B.
В този случай условната вероятност на събитието A при условие B е равна
на безусловната вероятност на A.
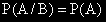
Ако събитието A е независимо от B то и B е независимо от A.
Ако A и B са независими, то
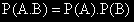
Типични независими събития са:
Изваждане с връщане.
Последователно хвърляне на монета.
Последователна стрелба по мишена.
Пример:
Хвърлени са два зара. Намерете вероятността на първия зар да се е паднало 2,
при условие, че сумата на точките е по-малка от 6.
Независими ли са тези све събития?
Решение:
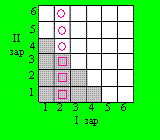
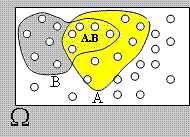
На чертежа, с розова фигура са представени елементарните събития
от събитието A - на I зар има 2 точки,
а със сив цвят тези от B - сумата е по-малка от 6.
|W|=36; |A|=6; |B|=10; |AB|=3.
Вероятността на A при условие B е равна на:
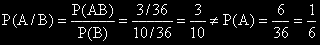
Следователно, двете събития са зависими.
Другият пример е от застрахователната математика
Да разгледаме долната графика.
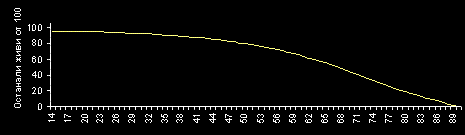
По абцисата са нанесени възрасти – t а по ординатата процентите от родените
в една и съща година индивиди, преживели съответната възраст – s(t).
Тази функция се нарича " функция на оцеляването" (survival function).
Долната графика е взета от книгата " Основы страховой математики" – автор Г. М. Кошкин и касае годината 1984.
По съвременни данни могат да се намерят в страниците
"http://demoscope.ru/"
"http://www.mortality.org/"
Жалко, че в страницата на Българския национален статистически институт подобни данни няма.
С 1 означаваме събитието произволно избран от популацията индивид да преживее настоящата година.
Вероятността за това зависи от неговата възраст – T – събитие, което ще означим с .
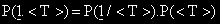
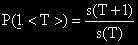
Вероятността P(< T >) се определя от т.н. възрастова пирамида.
По вертикалната скала се задава възрастта, а дължината на хоризонталната ивица
определя вероятността случайно избран индивид да е от тази възрастова група.
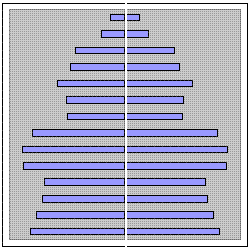
Тази примерна възрастова пирамида е заимствана от горните източници.
При нея първият възрастов интервал е 15-19 год. а последният – 85 – 90.
Дай Боже всекиму.
Какво ще научим:
Формула за пълната вероятност
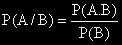
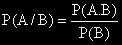

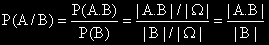
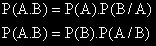
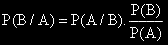 , защото:
, защото: