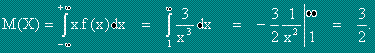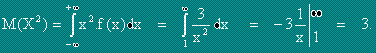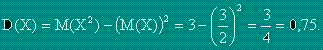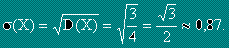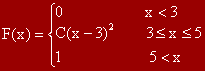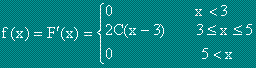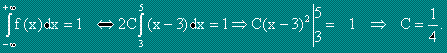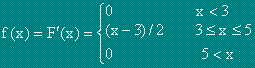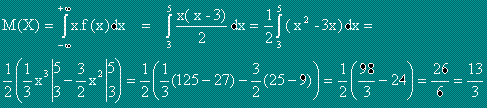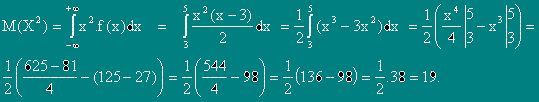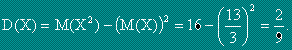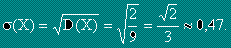Числови характеристики на непрекъсната случайна величина -
математическо очакване и дисперсия

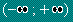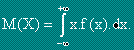
Нека f(x) е плътност на разпределение на непрекъснатата случайна величина X. Математическо очакване M(X) (или средна стойност ) на X се нарича интегралът от произведението x.f(x), като интегрирането се извършва във границите . Дисперсия ( разсейване ) на случайната величина X се нарича математическото очакване на квадрата на отклонението на случайната величина от нейното математическо очакване. 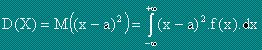, където a=M(X). 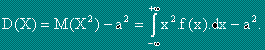Доказва се, че: Стандартно отклонение - s(X) се нарича корен квадратен от дисперсията.

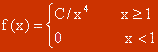
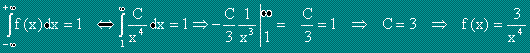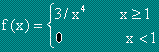Пример 1. При каква стойност на параметъра C, функцията: може да бъде плътност на разпределение на някоя непрекъсната случайна величина X ? Намерете константата C , M(X) и D(X).

Скицираме графиката на y = f(x), която трябва да бъде плътност на разпределение на X. , при x по-голямо или равно на 1. Така, че .

Пример 2. Дадена е функцията на разпределение на непрекъсната случайна величина. а) Намерете коефициента C. б) Намерете плътността f(x) на разпределение на случайната величина X. в) Намерете M(X) и D(X).

Намираме плътността на разпределение, която е производната на функцията на разпределение F(x). Интегралът на тази плътност, в границите трябва да е 1. Така намираме C: Така, че: