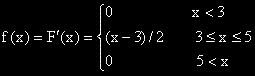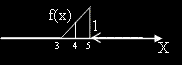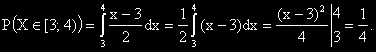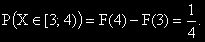
 е равна на нула.
е равна на нула.
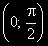 а случайната величина е sin(a).
а случайната величина е sin(a).
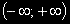 и нека F(x) е такава функция,
за която е изпълнено:
и нека F(x) е такава функция,
за която е изпълнено:
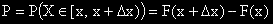 .
.

| 1. | 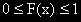 |
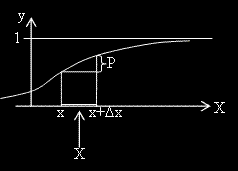
F(x) заема стойности между 0 и 1. |
| 2. | 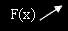 |
F(x) е растяща функция. |
| 3. | 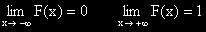 |
F(x) клони към 0 при x клонящо към минус безкрайност и към 1 при x клонящо към плюс безкрайност. |
| 4. | F(x) е непрекъсната функция. | |
| 5. | 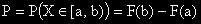 |
Вероятността сл. вел. X да приеме стойност между a и b е равна на F(b) - F(a). |
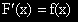 .
.
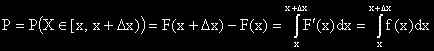 .
.
| 1. | 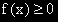 |
f(x) е неотрицателна. |
| 2. | 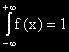 |
f(x) е нормирана. |
| 3. | 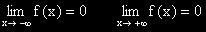 |
f(x) клони към 0 при x клонящо към минус или плюс безкрайност. |
| 4. | 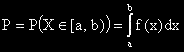 |
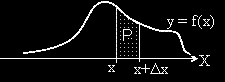
Вероятността случайната величина X
да приеме стойност между a и b е равна на лицето на криволинейния трапец ограничен от вертикалните прави x = a и x = b. |
| 5. | 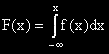 |
Функцията на разпределение е примитивна на функцията на плътността f(x). |
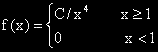
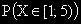
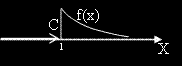
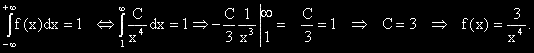
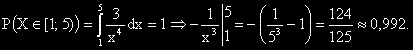
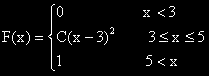
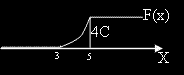
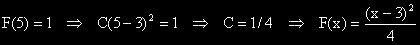 в интервала между 3 и 5.
в интервала между 3 и 5.