"Късче по късче / на деня от твърд’инята / своето щастие / откъртваме / ний;
троха по троха / го събира Родината / и глътка по глътка / сладко го пий."
- Пеньо Пенев
Какво трябва да знаем:     Биномно разпределение и схема на Бернули       Случайни величини      
Числови характеристики на дискретна случайна величина - математическо очакване и дисперсия      
Редове на Маклорен за елементарни функции - таблица   		Теория на вероятностите
Висша математика III част

Поасоново разпределение

Нека случайна величина X може да заема само натурални стойности {0, 1, 2, 3 ...n ...} с вероятности , където λ е положителен параметър.
Сумата на pn n=0,1,2... е единица така че тези числа са вероятности на разпределение.
Това следва от развитието на показателната функция в степенен ред.

      Това разпределение е било разгледано от Поасон (Симон Денис Поасон 1781 - 1840 ) . Към края на своя живот той се интересувал от приложенията на теорията на вероятностите и статистиката в администрацията и практиката в правото. Съдебните архиви съдържали много метериали, годни за статистически изследвания. В труда си „Приложение на вероятностите в съдебната практика” той въвежда означението pk(λ) като гранична вероятност за биномното разпределение.

      По-точно е доказал, че при нарастване на броя на опитите и промяна на вероятността за „успех” така, че произведението им да клони към λ вероятността за k „успеха” клони към вероятността за k събития на Поасоново-разпределена случайна величина.

Изразът в първите скоби клони към единица при n клонящо към безкрайност. което се вижда от разлагането:
Изразът във вторите скоби клони към e-λ при n клонящо към безкрайност.

Поасоновото разпределение разкрива своите предимства при статистическите явления свързани с относително редки явления в определен интервал (времеви или пространствен).
  1. Настъпване на застрахователно събитие в определен период от време
  2. Брой дефекти на определена дължина кабел
  3. Заболяване или смърт при даден брой жители
  4. Цялата застрахователна математика е основана на Поасоновото разпределение
  5. Теория на масовото обслужване

Ето два примера от далечното време, в което България имаше индустрия.
1 Завод за електрокари произведа продукция с вероятност за брак 0,01.
Каква е вероятността от 300 изделия 3 да бъдат бракувани.
При означенията на Биномното разпределение n=300, k=3 и p=0,01.
n.p е равно на 300.0,01=3.
Това е параметърът лабда на Поасоновото разпределение

2 Вероятността за дефект на един линеен метър силов кабел, произведен от кабелен завод „Васил Коларов” – Бургас, преди неговата приватизация е била 0,001.
Каква е вероятността за 4 и повече дефекта при кабел с дължина 3000 метра.
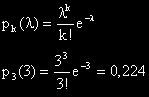
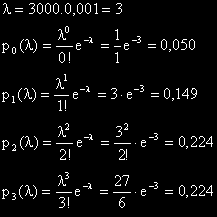
Събирайки тези резултати получаваме 0,647 – вероятността да има по-малко от 4 дефекта на 3 км. дължина.
Вероятността на противоположното събитие е 1-0,647= 0,353.
Една задача с по-съвраменна фабула.
Но оживено кръстовище, по което минават 1 000 автомобила дневно могат да се случат леки, средни и тежки катастрофи.
Техните вероятностите за един ден, заедно с техните цени са дадени в долната таблица.
Цената за построяване на светофар, заедно с неговата подръжка е 15 000.
Наличието на светофар коства 10 ст. преразход на гориво от всеки преминаващ през кръстовището автомобил.
Струва ли си светофарът да баде поставен?

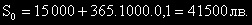
Да изчислим разходите и загубите при поставяне на сфетофар: - Разходи –Ex2_1
Да разгледаме разходите при липса на сфетофар:
За един вид катастрофа ще определим вероятностите за 1 , 2 , 3 и т.н. на брой катострофи и всяка от тях ще умножим по съответните материалните разходи.
Така ще знаем материалните загуби, причинени от катастрофи.
Параметърът на Поасоновото разпределение за тежките катастрофи е λ1 = 365.0,003=1,095.
Нека L1 материалната цена на една тежка катастрофа. Тогава загубите, причинени от тежките катастрофи са:
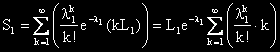
Да съкратим на k и да изкараме λ1 пред сумата:
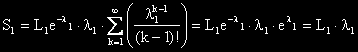
Сумата е:
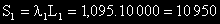
По същия начин изчисляваме загубите от средни и леки катастрофи.

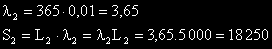
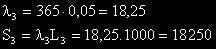
Общите загуби от катастрофи са:

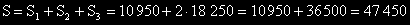
Това показва, че поставянета на сфетафар, финансово погледнато, е безсмислено.
И от друга страна – струва ли си да намаляваме скоростта на бизнеса!?
Доказва се, че средната стойност и дисперсията на Поасоновото разпределение са равни на λ.
Какво ще научим:    
Сметало за разпределението на Поасон 		Теория на вероятностите
Висша математика III част