Съдържание
Какво трябва да знаем:
Тригонометрични функции за сбор и разлика на ъгли
Тригонометрична форма на комплексните числа
Действия с комплексни числа записани в тригонометрична форма
1 Комплексно спрягане
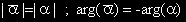
2 Умножение
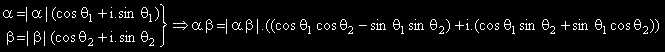
От тригонометричните формули за
сума
на ъгли следва, че реалната и имагинерна части са съответно:
cos(q1+q2) и
sin(q1+q2)
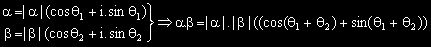
Модулът на произведението на две комплексни числа е произведение от модулите,
а аргументът му е сума на аргументите.

Фигуративно точката, представяща числото a се завърта около началото на
координатната система - т. O на ъгъл argb и се отдалечава от O
|b| пъти.
3 Степенуване
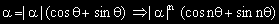
4 Деление
Да припомним, че
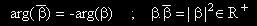
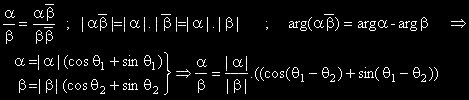
Изводът е че модулът на частното на две комплексни числа е частното от техните модули а аргументът му е разлика от техните аргументи.
Пример: Опростете израза: 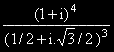
Решение:
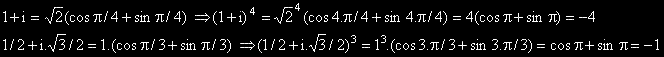
Отговорът е -4/-1 = 4.
Какво ще научим:
Коренуване в C Формула на Моавър
Съдържание