Съдържание
Какво трябва да знаем:
Дефиниция на тригонометричните функции
Комплексни числа - алгебрична форма
Тригонометрична форма на комплексните числа
Нека комплексното число a е изобразено като точка A в Гаусовата равнина.
Точката A е с координати a и b. Разстоянието OA е равно на модулът на a.
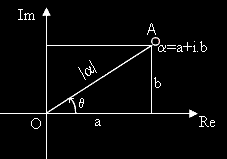
Ъгълът между лъчите ORe и OA се нарича аргумент на a и се означава с arg(a).
Той е дефиниран с точност до 2.p.
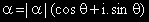
Тази форма на запис се нарича тригонометрична форма на a.
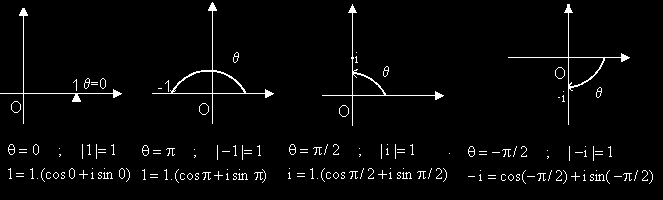
Пример: Ще намерим тригонометричните форми на 1+i и 1-i:
Нанасяме ги в Гаусовата равнина и извършваме съответните изчисления:
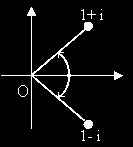
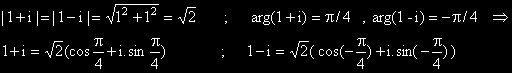
Задача: Намерете тригонометричните форми на числата:
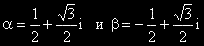
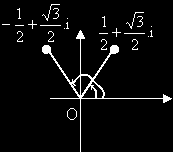
Какво ще научим:
Действия с комплексни числа в тригонометрична форма
Съдържание