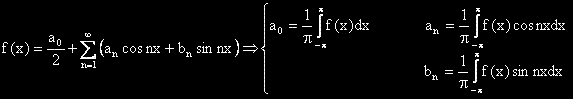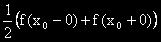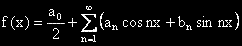
в интервала (-p, p).
| Какво трябва да знаем:
Определени интеграли, свързани с редовете на Фурие |
Съдържание на висша математика I част Съдържание на висша математика II част Съдържание на висша математика III част |
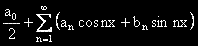 се нарича тригонометричен ред.
се нарича тригонометричен ред.
[1]
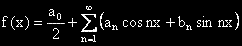
в интервала (-p, p).
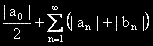
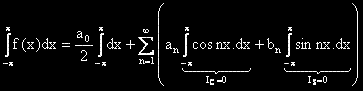
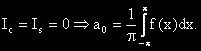
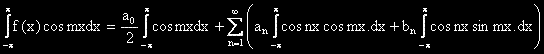
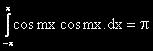 .
.
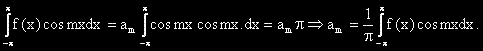
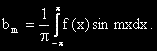
[2]