Линейни нехомогенни диференциални уравнения с постоянни коефициенти (ЛнХДУпк)
със специална дясна част
Те са от вида:
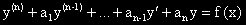 , където f(x) е функция от вида:
, където f(x) е функция от вида:
I. 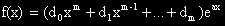 или
или
II. 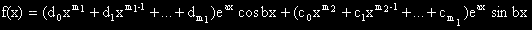
На всяка специална дясна част съответства едно число.
В първия случай е реалното число "a" а във втория – комплексно – спрегнатата двойка "a  ib".
ib".
Ако a или a  ib, съответно в I-ия или II-ия случай, не е корен на ХУ, то частното решение (ЧР) се търси във вида:
ib, съответно в I-ия или II-ия случай, не е корен на ХУ, то частното решение (ЧР) се търси във вида:
I. 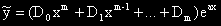 или
или
II. 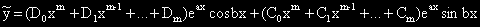 ,
,
където m = max(m1,m2).
Ако a или a  ib, съответно в I-ия и в II-ия случай, е корен на ХУ от кратност r,
то частното решение е от вида: x r
ib, съответно в I-ия и в II-ия случай, е корен на ХУ от кратност r,
то частното решение е от вида: x r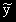 .
.
Неизвестните коефициенти Di или Di и Ci се определят,
като се замести в изходното ЛнХДУпк и се приравнят коефициентите пред
изразите от вида: x i.eax в I-ия,
или пред xi.eax.cosbx и
x i.eax.sinbx във II-ия случай за равните i от двете страни на равенството.
При дадена специална дясна част, числото, което 'и съответства, ще отбелязваме в скоби, вдясно от нея.
Определете общия вид на ЧР при дадената специална дясна част (лявата е означена с многоточие):
Задача 1. ... = x 2e3x.
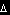 (Решение:) (3) Ако 3 не е корен на ХУ, то:
(Решение:) (3) Ако 3 не е корен на ХУ, то: 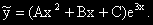
Ако 3 е корен на ХУ от кратност r, то: 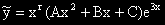 .
.
И двата случая могат да се обединят в: 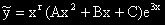 ,
,
където r е кратността на корена 3 в ХУ или нула, ако 3 не е корен на ХУ.

Задача 2. . . . = x.
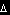 x = x.e0x (0) Ако 0 не е корен на ХУ, тo:
x = x.e0x (0) Ако 0 не е корен на ХУ, тo: 
Ако 0 е корен на ХУ от кратност r, то: 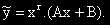
И двата случая могат да се обединят в:  , където r е кратността на 0 в ХУ.
, където r е кратността на 0 в ХУ.

Задача 3 . . . . = (x2 + x)cosbx + x.sinbx.
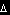 ( 0
( 0  bi )
bi ) 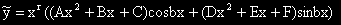 ,
където r е кратността на
,
където r е кратността на  bi в ХУ.
bi в ХУ.

Задача 4. . . . = x.e2xcosx + е2xsinx.
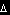 ( 2
( 2  1.i ) .
1.i ) .
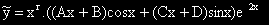 , където r е кратността на 2
, където r е кратността на 2  i в ХУ.
i в ХУ.

Задача 5. . . . = x.sinx + cos2x.
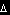 Тук трябва да се използва принципът на суперпозицията (ПС).
Тук трябва да се използва принципът на суперпозицията (ПС).
Разглеждаме две уравнения с еднаква лява част, а дясна - съответно: x.sinx ( i) и
cos2x (
i) и
cos2x ( 2i), с частни решения съответно:
2i), с частни решения съответно:
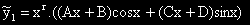
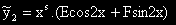 ,
,
където r и s са кратностите на
 i и
i и  2i в ХУ.
2i в ХУ.
Тогава: 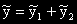 .
.

За посочените ЛнХДУпк напишете вида на ЧР, без да ги решавате:
Задача 6. 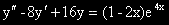 .
.
 (4) ХУ е:
l2 - 8l + 16 = 0
(4) ХУ е:
l2 - 8l + 16 = 0
 (l - 4)2 = 0.
(l - 4)2 = 0.
4 е корен на ХУ от кратност 2
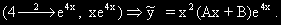

Задача 7. 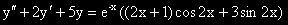 .
.
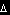 (-1
(-1  2i)
2i)
ХУ е: l2 + 2l + 5 = 0.
l1,2 = -1  2i.
2i.
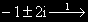 (-1
(-1  2i е корен на ХУ от кратност 1)
2i е корен на ХУ от кратност 1)
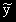 = xe-x((Ax + B)cos2x + (Cx + D)sin2x) .
= xe-x((Ax + B)cos2x + (Cx + D)sin2x) .

Намерете ОР на ЛнХДУпк:
Задача 8. 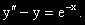
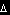 (-1) ХУ е: l2 - 1 = 0.
(-1) ХУ е: l2 - 1 = 0.
 (l - 1)(l + 1) = 0.
(l - 1)(l + 1) = 0.
ОР на ЛХДУ е: y0 = C1ex + C2e-x.
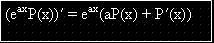
-1 е корен от кратност 1 на ХУ * 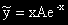 .
.
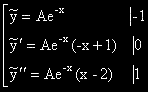
(отдясно са показани коефициентите пред производните в изходното уравнение)
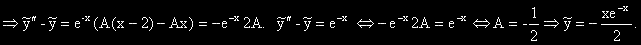
ОР на изходното ЛнХДУпк е: 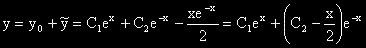 .
.

Задача 9. 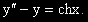
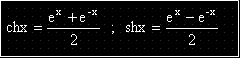
 ДУ
ДУ 
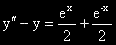 .
.
От 3ад. 8 ОР на ЛХДУпк е: y0 = C1ex + C2e-x.
За намиране на ЧР трябва да приложим ПС.
Търсим ЧР на уравненията:
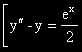 (1)
(1) 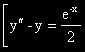 (-1)
(-1)
(в скоби са указани числата, които съответсват на специалната дясна част)
Поради това, че  1 са корени на ХУ от кратност 1, ЧР-ия са от вида:
1 са корени на ХУ от кратност 1, ЧР-ия са от вида:
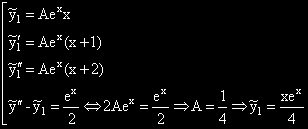

От ПС получаваме ЧР: 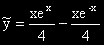 .
.
ОР на изходното ДУ е: 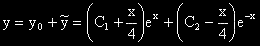 .
.

Задача 10. 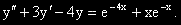
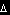 ХУ е:
l2 + 3l - 4 = 0
ХУ е:
l2 + 3l - 4 = 0
 (l + 4)(l - 1) = 0.
(l + 4)(l - 1) = 0.
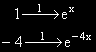
ОР на ЛХДЕ е: y0 = C1ex + C2e-4x.
Търсейки ЧР, отново използваме ПС:
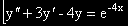 (-4)
(-4) 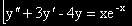 (-1)
(-1)
[ -4 e 1-кратен корен на ХУ [-1 нe е корен на ХУ
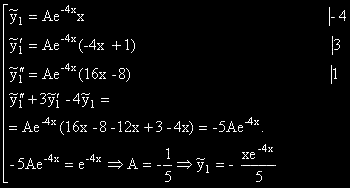
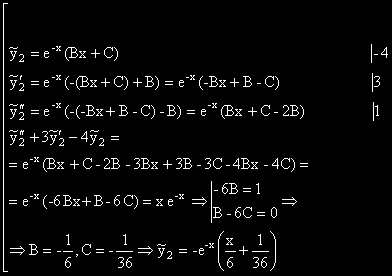
ОР на изходното ДУ е: 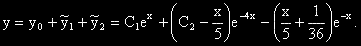

Задача 11. 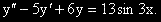
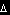 (
( 3i)
ХУ е: l2 - 5l + 6 = 0
3i)
ХУ е: l2 - 5l + 6 = 0
 (l - 2)(l - 3) = 0
(l - 2)(l - 3) = 0
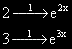
ОР на ЛХДУ е: y0 = C1e2x + C2e3x.
 3i не е корен на ХУ
3i не е корен на ХУ 
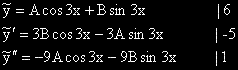
Заместваме в ЛнХДУ: 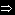
(-9A - 15B + 6A)cos3x + (-9B + 15A + 6B)sin3x = (-3A - 15B)cos3x + (15A - 3B)sin3x = 13sin3x 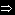
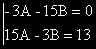
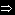
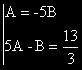
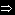
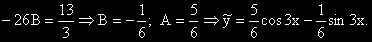
ОР на изходното ДУ е:
y = C1e2x + C2e3x + 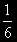 (5cos3x - sin3x) .
(5cos3x - sin3x) .

Задача 12. 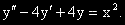
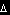 (0)
ХУ е: l2 - 4l + 4 = 0
(0)
ХУ е: l2 - 4l + 4 = 0
 (l - 2)2 = 0
(l - 2)2 = 0
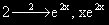
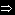 ОР на ЛХДУ е: y0 = (C1 + C2x)e2x .
ОР на ЛХДУ е: y0 = (C1 + C2x)e2x .
0 не е корен на ХУ 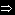 ЧР е от вида:
<
ЧР е от вида:
< 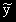 = (Ax2 + Bx + C)e0x = Ax2 + Bx + C.
= (Ax2 + Bx + C)e0x = Ax2 + Bx + C.
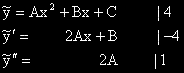
Заместваме в ЛнХДУ: 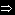
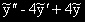 =
=
2A - 4(2Ax + B) + 4(Ax2 + Bx + C)= 4Ax2 + (-8A + 4B)x +2A - 4B + 4C = x2 + 0x + 0 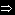
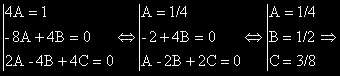
ОР на изходното ДУ е: y = (C1 + C2x)e2x + 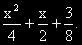

Полезна, в общия случай, при изчисляване на производните на 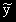 е следната формула:
е следната формула:

В частен случай, при r = 0, се получава формулата:
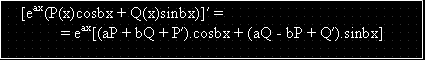
Задача 13. Намерете ЧР на ДУ 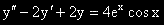 ,
,
което удовлетворява началните условия:
y(p) = pep
и y'(p) = ep.
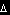 (1
(1  i)
ХУ: l2 - 2l + 2 = 0.
l1,2 = 1 * i
i)
ХУ: l2 - 2l + 2 = 0.
l1,2 = 1 * i
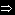 y0 = (C1cosx + C2sinx)ex .
y0 = (C1cosx + C2sinx)ex .
1  i е корен на ХУ
i е корен на ХУ 
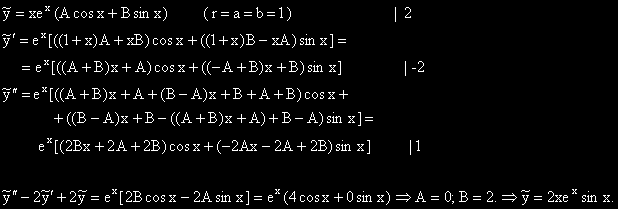
ОР на изходното ДУ е: y = ex (C1cosx + (C2 + 2x)sinx).
y' = ex((C1 + C2 + 2x)cosx + (C2 + 2x + 2 - C1)sinx).
y(p) = pep
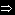 ep(-C1) = pep
ep(-C1) = pep
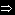 C1 = -p.
C1 = -p.
y'(p) = ep
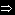 ep(-(C1 + C2 + 2p)) = ep
ep(-(C1 + C2 + 2p)) = ep
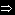 C2 = 1 - C1 - 2p = -1 - p
C2 = 1 - C1 - 2p = -1 - p
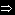 y = ex(-pcosx + (2x - p - 1)sinx) .
y = ex(-pcosx + (2x - p - 1)sinx) .

Задача 14. Да се докаже, че ако р не е корен на ХУ на ЛнХДУпк: a0y'' + a1y' + a2y = Cepx,
то:
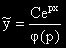 , където
, където 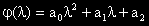 е ЧР на ЛнХДУ.
е ЧР на ЛнХДУ.
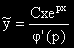 ако р е еднократен корен на ХУ и
ако р е еднократен корен на ХУ и
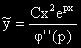 ако р е двукратен корен на ХУ.
ако р е двукратен корен на ХУ.
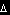 Ако р не е корен на ХУ то:
Ако р не е корен на ХУ то:
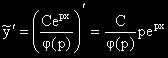 .
.
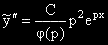 .
.
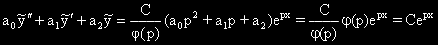 .
.
Във втория случай
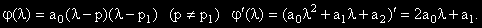 .
.
Тогава: 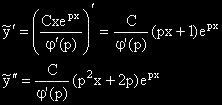 .
.
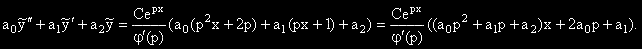
Но изразът във вътрешните скоби е 0, поради това че р е корен на ХУ.
Изразът извън скобите е 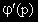 , така че се получава: C.epx.
, така че се получава: C.epx.
В третия случай 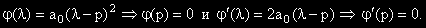 . Тогава:
. Тогава:
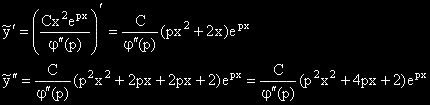
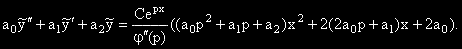
Но изразите във вътрешните скоби са съответно 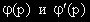 , които са 0,
а изразът извън скобите е
, които са 0,
а изразът извън скобите е 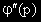 , така, че отново се
получава C.epx.
, така, че отново се
получава C.epx.

Задача 15. Да се намери ЧР на ЛнХДУпк: 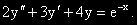
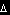 C = 1, p = -1. -1 не е корен на ХУ
C = 1, p = -1. -1 не е корен на ХУ

Какво ще научим:
Вече всичко знаем.