Решения на типични изпитни задачи по Аналитична геометрия

Задача 1
Да се намери уравнението на права , минаваща през пресечната точка на правите с уравнения x=y/2 и
3x+y-5=0 и перпендикулярна на правата с уравнение: 5x-8y+10=0.

(Тази задача беше дадена на изпит и не беше решена от никой. Срам за преподавателя.)
Решение

Задача 2
Координатите на два съседни върха на успоредник са А(-3, 6) и B (5, -4).
Пресечната точка на диагоналите му е О (-1, 2). Да се намерят:
- координатите на останалите два върха на успоредника
- косинуса на ъгъла при връх А
- лицето на успоредника АВCD
- абсцисата на точка от правата АВ с ордината 0

Решение

Задача 3
Да се намерят координатите на т. В, която е симетрична на т. А (-2,1) относно правата g: 4х + у - 9 = 0

(Предложени са три, еднакво важни решения.)
Първо pешение  Второ pешение  Трето pешение

Задача 4
Лицето на триъгълник е 1,5. Два от върховете му са A(2,-3) и B(3,-2).
Центърът на тежестта му лежи на правата 3x-y-8=0.
Намерете координатите на третия връх на триъгълника.

Решение

Задача 5
Страните на един триъгълник имат уравнения 4x-y-7=0 ; x+3y-31=0 и x+5y-7=0.
Намерете координатите на ортоцентъра му.

Решение

Задача 6
Да се съставят уравненията на страните на триъгълник ABC по дадени : връх A(4,-3),
височината през върха C : hC: 3x – y – 13 = 0 и
ъглополовящата през върха B: lB: x – y +1 = 0

Решение

Тест по основна математиката в канадско училище.

Класът съответства на нашия десети клас
Тематиката е от елементарна Аналитична геометрия
При преводът се приемат и използват нашите означения, запазвайки стила на изложението.
В оригинала е оставено е място за коменатари и въпроси.

Полезни формули


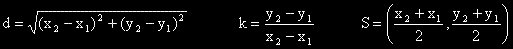
1. Намерете разстоянието между точките (-10,3) и (5,-4). Отговорете точно. (2 точки)

2. Намерете средата на отсечката с краища: (-10,3) и (5,-4). (2 точки)

3. Намерете наклонът на правата, минаваща през точките (-10,3) и (5,-4). (2 точки)

4. Вярно ли е че отсечката AB, с координати (4,2) и (-6,7) е успоредна на отсечката CD с координати (-4,11) и (-4,-5)? Да или не. Обосновете отговора си. (2 точки)

5. Ако отсечката AB с координати (3,7) и (-8,3) е перпендикулярна на CD, какъв е наклонът на CD? (2 точки)

6. Наклоните на 2 линии са 5/x и -3/4 . Намерете неизвестното ако двете линии са
a) успоредни (2 точки)

b) перпендикулярни (2 точки)

7. Ако една линия има наклон -5/2 и минава през точката (2,5), какви са координатите на пресечната точка с
a) оста x (2 точки)
b) оста y (2 точки)

8. Двама човека тръгват от една и съща точка но единият върви 2 пресечки на изток и 4 на юг а другият - 4 пресечки на север и 4 на запад. После спират. Какво е разстоянието между тях? (2 точки)

9. Отсечката AB има координати (-2,-1) и (6,3). Намерете координатите на трите точки, които разделят отсечката AB на четири равни части. (3 точки)

10. Назовете максимално точно четириъгълника с координати A(0,0), B(2,2), C(8,5) и D(-2,-5). (2 точки)

Отговори на теста

Решение на задача 1
Правим чертеж и план за решението на задачата.
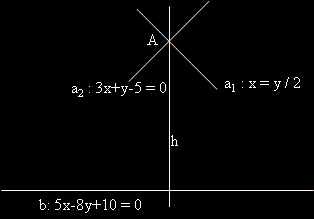
  1. Намираме координатите на пресечната точка на правите a1 a2 , като решим системата, образувана от техните уравнения.
  2. Определяме ъгловият коефициент на правата b и от условието, че b и h са перпедикулярни определяме ъгловият коефициент на h.
  3. Определяме уравнението на h, като уравнение на права, минаваща през точка с даден ъглов коефициент.

  1.    

  2.    

  3.    

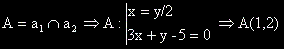
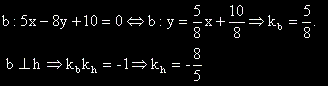
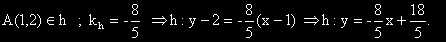
Решение на задача 2


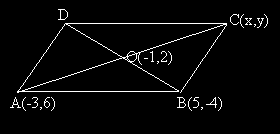
Да означим, временно координатите на C с x и y.
Понеже точка O е среда на AB, то x = 1 и y = -2.
Аналогично намираме координатите на т. D – (-7,8).


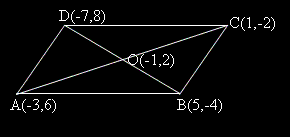
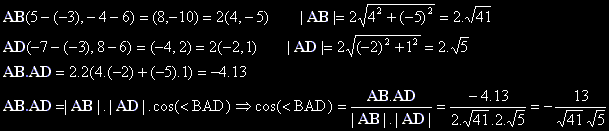
(Виж координати на вектор и скаларно произведение.)

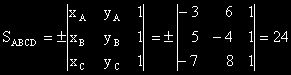
Накрая ще намерим абсцисата на точка от правата АВ с ордината 0.
Ъгловият коефициент на правата ABе:

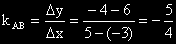
(Виж Декартово уравнение на права.)

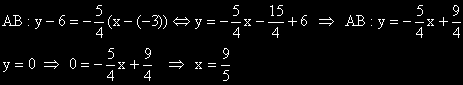
Първо решение на задача 3
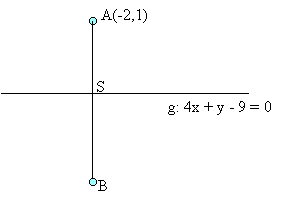
  1. Определяме ъгловият коефициент на правата g и от условието, че AB и g са перпедикулярни определяме ъгловият коефициент на AB.
  2. Намираме уравнението на правата AB, като уравнение на права, минаваща през точка A с даден ъглов коефициент.
  3. Намираме координатите на пресечната точка –S на правите AB и g , като решим системата, образувана от техните уравнения..
  4. От условието, че S е среда на отсечката AB намираме координатите на B.
  1.    

  2.    

  3.    

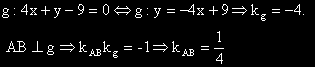
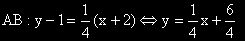
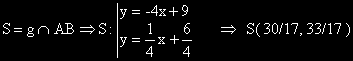
  4.     Нека B(x,y). S е среда на AB. Тогава:
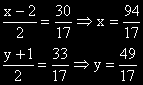
Отг. B ( 94/17, 49/17 )
Второ решение на задача 3
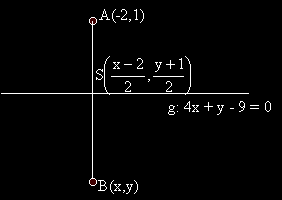
  1. Ако B има координати (x,y) са ни необходими две уравнения за определяне на неизвестните.
    Първото от тях е условието средата S на отсечката AB да лежи на правата g.
  2. Второто отразява факта, че g и AB са перпендикулярне и следователно ъгловият коефициент на правата AB е 1/4.
  3. Решаваме получената система.
   


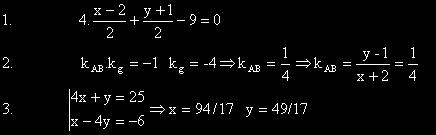
Трето решение на задача 3
  1. Определяме единичен вектор ng , колинеарен на правата g използвайки общото и уравнение.
  2. Нека C е произволно точка от g. Определяме векторът CS. Скаларното произведение (CA. ng ) е неговата дължина така, че
    CS=(CA.ng) . ng
  3. AS = CS - CA ; AB=2.AS и оттук определяме координатите на точка B.

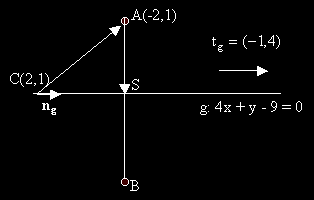
  1. Векторът tg с координати (-1, 4) е успореден на g (Виж Общо уравнение на права.)
       

  2.    

  3.    


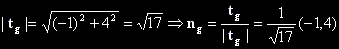
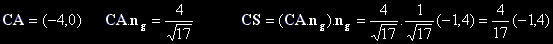
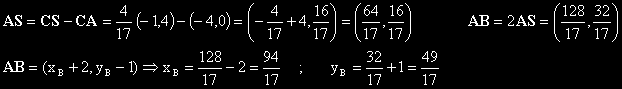
Решение на задача 4
Нека третия връх на триъгълника е C(x,y).
Координатите на медицентъра G са средноаритметични на координатите на върховете му.
Тогава:    

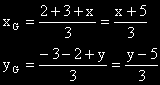
Тези координати трябва да удовлетворяват уравнението: 3x-y-8=0. Следователно:    

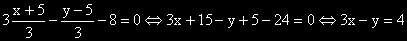
От друга страна лицето на триъгълника е 1,5.    

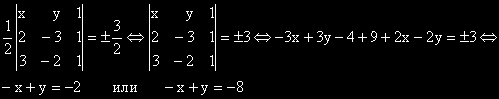
Решавайки двете системи получаваме две решения:
   
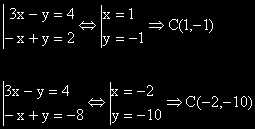
Решение на задача 5

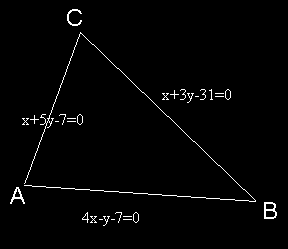
  1. Намираме координатите на два от върховете на триъгълника.
  2. Намираме ъгловите коефициенти на срещуположните им страни.
  3. Намираме уравненията на две от неговите височини.
  4. Тяхната пресечна точка е търсеният ортоцентър.

   

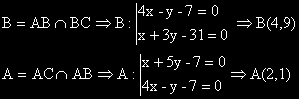
BC:x+3y-31=0 , откъдето следва, че BC:y=-1/3x+31/3.
Ъгловият коефициент на височината през A е равен на 3 и нейното уравнение е:
hA : y-1=3(x-2), еквивалентно на : hA : y=3x-5.
(Виж Уравнение на права през точка с даден ъглов коефициент.)
hB : y-9=5(x-4), еквивалентно на : hB : y=5x-11.
Решавайки системата, определена от двете уравнения, намираме координатите на ортоцентъра: H(3,4). Решение на задача 6

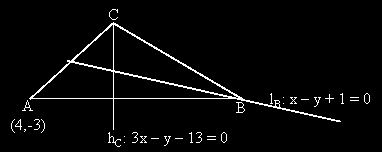
1) Уранението на AB
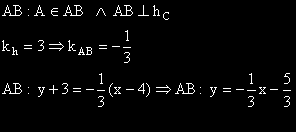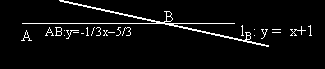2) Координатите на точка B, като пресечна точка на две прави
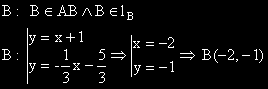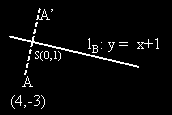3) Намираме ортогонално-симетричната точка на A спрамо lB .
Тази точка лежи на страната BC.

3а)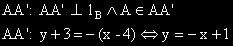
3б) Определяме координатите на точка S - пресечна на правите AA' и lB.      
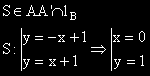
3в) Намираме координатите на A' от условието, че S е среда на AA'. 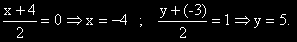A' (-4, 5)
4) Намираме уравнението на страната BC, определена от двете точки B и A', като уравнение на права през две точки.

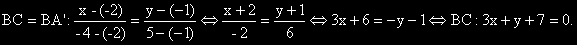
5) Намираме координатите на точка C, като пресечна точка на правите hC и BC.

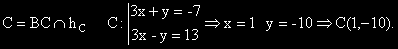
6) "Свързваме" точките A и C, за да определим уравнението на последната страна AC.


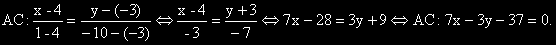
Отг. AB: 3y = - x - 5 ; BC: 3x+y+7=0 ; AC: 7x-3y-37=0

Отговори на теста
1. 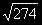            2.     (-5/2;-1/2)         3.     -7/15         4.     Не
5.     -11/4         6.     а) -20/3     б) -15/4         7.     а) x = 4     б) y = 10         8.     10
9.     (0,0) ; (2,1) ; (4,2)         10.     Трапец