Какво трябва да знаем:
Уравнение на права

Декартово уравнение на права

Декартово уравнение на права - определение

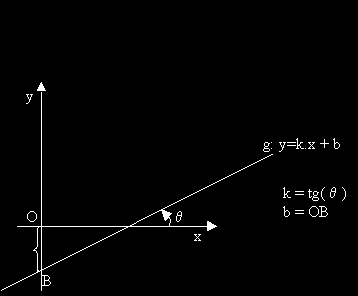
Декартовото уравнение на права е от вида g : y = k.x + b.
k се нарича ъглов коефициент а b - отрез по y.
Ъгловият коефициент е равен на тангенса на ъгъла, който сключва оста Ox с правата g
а b е ординатата на пресечната точка на правата с оста Oy.

Намиране на ъгловия коефициент на права по две дадени точки

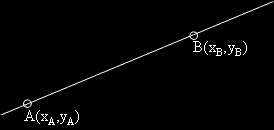
Ъглови коефициент

Ъгловият коефициент на правата, определена от две точки е равна на отношението на разликата на игреците и съответната разлика на хиксовете.

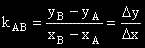
Ъглови коефициент

Уравнение на права през дадена точка с даден ъглов коефициент

Ако за правата g е известно че има ъглов коефициент k и че минава през точката A с координати x₀ y₀ ,
то уравнението на g е g: y-y₀ =k(x- x₀ )

Действително, ясно е че ъгловият коефициент на g е k и че координатите на точка A удовлетворяват това уравнение.

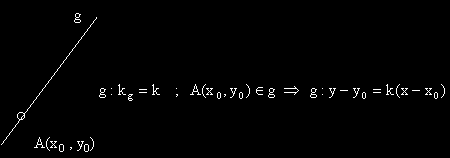
Уравнение на права през дадена точка с даден ъглов коефициент

Взаимно положение на две прави, зададени с Декартовите си уравнения

Ако две прави са успоредни, то ъгловите им коефициенти са равни.
Ако две прави са перпендикулярни, то произведението на техните ъглови коефициенти е равно на минус единица.

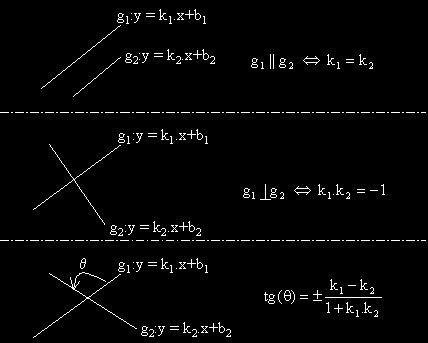
Взаимно положение на две прави, зададени с Декартовите си уравнения

Пример:
Дадена е права a с Декартово уравнение: a : y=2x-5 и точка A(-2,3).
Намерете уравнението на права p, минаваща през точка A и успоредна на правата a.
Намерете уравнението на права h, минаваща през точка A и перпендикулярна на правата a.

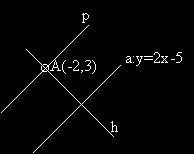
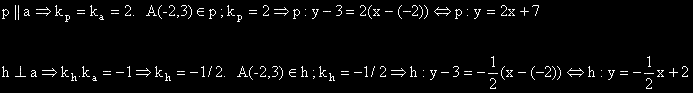
p||a ; h е перпендикулярна на a

Какво ще научим:
Уравнение на права през две точки
(канонично уравнение на права)