Съдържание на висша математика I част
Съдържание на Аналитична Геометрия
Какво трябва да знаем:
Декартово уравнение на права
Уравнение на права през две точки
Как се решават задачи по аналитична геометрия
Ето една фабула, който обикновено се разкрива пред студента на изпита.
Даден е един триъгълник с координатите на неговите върхове.
Да се намери
- уравнението на една негова страна
- уравненията на негова медиана или височина
- намиране на ортогонално симетричната точка на дадена точка спрямо дадена права
- намиране на връх на триъгълник при дадени други негови елементи
Какво е необходимо да се направи за решаването на задачата?
Три неща: (Има три вида математици – такива, които могат да броят и такива, които не могат.)
- Чертеж и нанасяне на данните от условието на него
- План за решаването на задачата
- Изпълнение на плана
- Красиво и прегледно оформяне на цялостното решение. Чрез това Вие показвате уважението си
към преподавателя и неговата науката, както и дълбочината на вашите знания.
При изложението на решението използвайте съответната терминология.
Изразявайте се кратко и научно, с внимателно обмислени изрази.
Тестовото изпитване изисква друг подход.
Задача: Даден е триъгълник A(-1,2) B(5,-6) C(1,2).
а) Намерете уравнението на медианата AM през върха A.
б) Намерете пресечната точка на медианата AM с височината CH през върха C.
Решение:
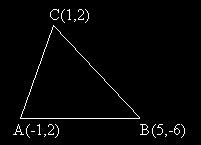
План за подусловие а)
I Намираме т. M от условието, че тя е среда на
отсечката BC
II Намираме уравнението на правата AM –
уравнение на права през две точки.
Помощен чертеж за подусловие а)
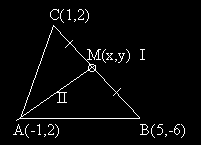
Символично изразяване на плана за подусловие а)
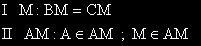
Изпълнение на плана за подусловие а)
I 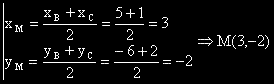
Нанасяме на помощния чертеж получените координати: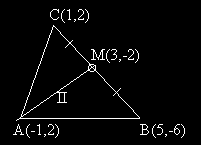
II
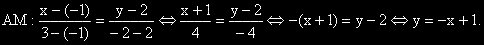
Проверката показва, че координатите на A и M удовлетворяват това уравнение.
Оформяне на решението за подусловие а)
Решение на подусловие а)
Точка М е среда на отсечката BC, откъдето следва, че тя има координати: (5+1)/2 = 3 и (2-6)/2 = -2.
Определяме уравнението на медианата AM, като права през две точки:
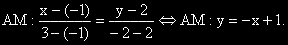
План за подусловие б)
- I Намираме уравнението на височината CH.
- II Намираме
пресечната точка на медианата AM, определена от а) и намерената от I височина - CH,
като пресечна точка на две прави.
Помощен чертеж за подусловие б)

Символично изразяване на плана за подусловие б)
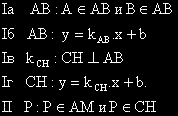
Изпълнение на плана за подусловие б)
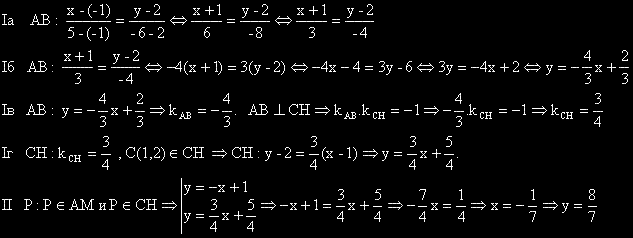
Оформяне на решението за подусловие б)
Определяме ъгловия коефициент на правата AB и от условието, че АВ е
перпендикулярна на CH
определяме kCH :
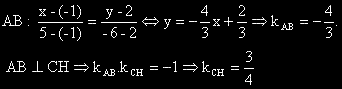
Намираме уравнението на правата CH и решаваме съответната система за определяне на координатите на
пресечната им точка P.
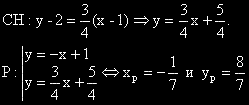
Забележка: Ъгловият коефициент на AB
може да се определи и директно чрез координатите на A и B.
Тази забележка може да я приемате отправена както към Вас, така и към Преподавателя, защото ако се беше сетил, би направил така.
Не виждам нищо сложно. Ако Вие виждате пишете ни.
Какво ще научим:
Отрезово уравнение на права
Общо уравнение на права
Общо уравнение на права