Уравнение на равнина през точка, успоредна на два вектора
Нека е дадена точка A( х0, y0, z0) и два неколинеарни
вектора t1(a1 , b1 , c1)
и t2(a2 , b2 , c2).
Търсим уравнението на равнина a,
съдържаща точката A( х0, y0, z0) и успоредна ( компланарна ) на векторите
t1(a2 , b2 , c2) и
t2(a2 , b2 , c2).
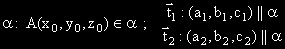
Ако точка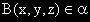 
, то векторът AB
е линейна комбинация на векторите
t1(a2 , b2 , c2) и t2(a2 , b2 , c2)
:
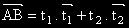, за определени числа t1 и t2 , които се наричат параметри.
Тогава, записвайки това равенство покоординатно получаваме:
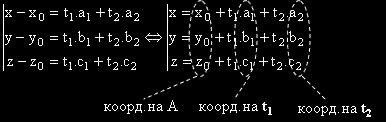
В това уравнение на a , наричано параметрично,
t1 и t2 са параметри.
Равнината има двупараметрично уравнение.
Може да се постъпи и така:
Векторът t1 x t2 , бидейки перпендикулярен и на двата свои
множителя е нормален (перпендикулярен) и на равнината a.
Той има координати:
,
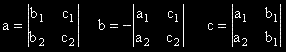и тогава общото уравнение на равнината a е :
a : a.(x - x0 )+ b.(y - y0 )+ c.(z - z0 ) = 0.
Пример
Намерете общото уравнение на равнина a, минаваща през точките A(1,2,3) и B(-1,2,1)
и успоредна на вектора t (-1,0,2).
Векторът AB(-2,0,-4) и колинеарният нему (1,0,2) е успореден на a.
Векторът n = t x AB с координати (0,-4,0) и колилнеарният нему (0,1,0) е перпендикулярен на
a.
Намираме уравнението на a от условията :
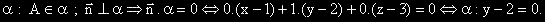
Какво ще научим:
Уравнение на права в пространството