По страницата се работи!
Сметало за специални функции, свързани с теорията на вероятностите
Функции и указания за работа
Функция на грешката се нарича интегралът
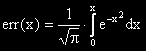
Функцията на нормално разпределена случайна величина със средна стойност 0 и дисперсия
1 се определя от равенството:
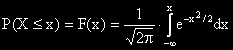
Ще я означаваме с p = N( n(0,1), x ).
Сметалото пресмята и стойносттта на неопределените интеграли:
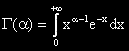 и на
и на
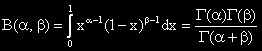
Те се наричат съответно Гама и Бета функция.
Въведени са от Ойлер.
Стойностите на аргумента на Γ трябва да са различни от 0 и от отрицателните, цели числа.
По абсолютна стойност те трябва да са по-малки от 20.
Ако разгледаме функция от горната граница на определения интеграл дефиниращ Гама функцията се получава функция,
зависеща от параметър α, която се нарича „непълна Гама-функция”:
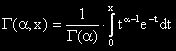
Тя е функция на Гама-разпределението.
Нейната обратна определя тази стойност y, за която при даден аргумент x между нула и едно е изпълнено:
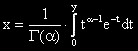 Ще я означаваме с
Ще я означаваме с
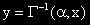
Непълна Бета-функция се дефинира с интеграла
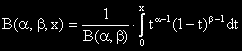
Означението на сметалото е "SΒ(α , β ,x)".
Тя е функция на Бета-разпределението.
Нейната обратна определя тази стойност y, за която при даден аргумент x между нула и едно е изпълнено:
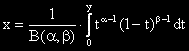
На сметалото ще я означаваме със "SΒ^(-1)(α , β ,x)".
F - разпределението (на Фишер, разпределене на Снедекор) е с плътност
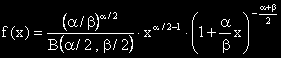
Величините α и β се наричат степени на свобода при F - разпределението.
χ2 разпределението е със плътност
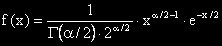
Плътността на t - разпределението (на Стюдент) е
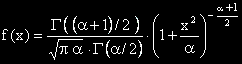
Изказвам благодарност на братушките за позволението да използвам техния код.
Ето ги къде се крият:
http://www.alglib.net/
Здраствуйте Братушки!
Самото сметало
Непълните Бета и Гама - функции и техните обратни не са проверени!