Посвещавам на студентите от висшето транспортно училище „Тодор Каблешков” - София
Преминаване от декартови в полярни,
цилиндрични и сферични координати при тройните интеграли - задачи
Задача 1. 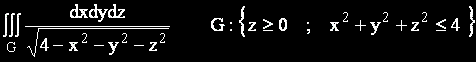
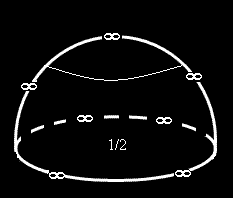
Областта на интегриране е горната част на полусфера с радиус 2.

Подинтегралната функция е безкрайност по точките от сферата а в нейния център е 1/2.
Преминаваме към сферични координати. Якобианът на този преход е ρ2sinψ.
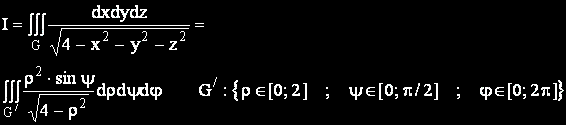
Новите граници на интегриране определят правоъгълна област, така че
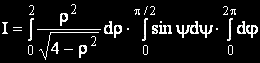
Последните два интеграла се решават лесно и тяхното произвдение е 2π.
Първият заслужава нашето специално внимание.
Ще решим определения интеграл
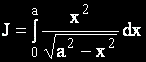
Полагаме x = asint. Интегралът придобива вида:
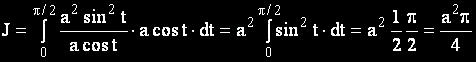
Окончателно получаваме:
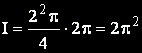
Задача 2. 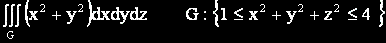
Областта на интегриране е слоят между двете централни сфери с радиуси 1 и 2.
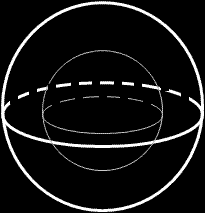
Преминаваме към сферични координати. Якобианът на този преход е ρ2sinψ.
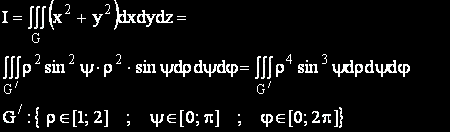
Новите граници на интегриране определят правоъгълна област, така че
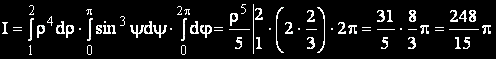
Задача 3. 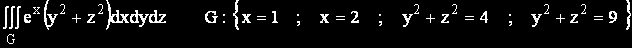
Повърхнината с уравнение
y2 + z2 = a2 представлява цилиндрична повърхност с
управителна крива
y2 + z2 = a2 ,
която е окръжност с център O и радиус a, разположена в равнината Oyz.
Четвърт от областта, заключена между две такива концентрични цилиндрични повърхнини е изобразена на чертежа.
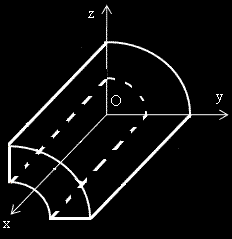
Равнините x=1 и x=2 са успоредни на равнината Oyz. Едната от тях може да се каже че е начертана.
Да начертаем и другата.
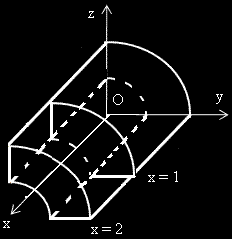
Сега вече нещата се изясняват.
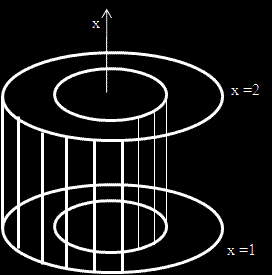
Може би е по-добре да изобразим координатната система така, че оста Ox да е нагоре.
И да не забравяме, че досега разглеждахме една четвърт от областта на интегриране.
Ситуацията в равнината Oyz е от ясна – по-ясна.
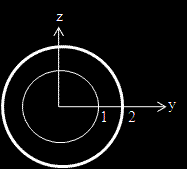
Преминаваме към полярни координати с "основа" равнината Oyz. Якобианът на този преход е ρ.
По точно е да кажем, че преходът е в цилиндрични координати чрез формулите
x = x y = ρcosφ z= ρsinφ
Но това не е съществено, защото якобианът на двата прехода е един и същ.
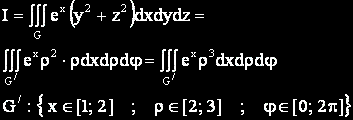
Новите граници на интегриране определят правоъгълна област, така че
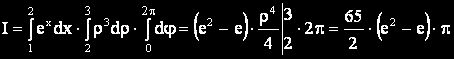
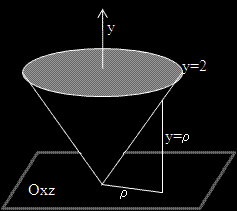
Задача 4. 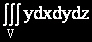 където V е областта, ограничена от коничнита повърхнина и равнината y = 2.
където V е областта, ограничена от коничнита повърхнина и равнината y = 2.
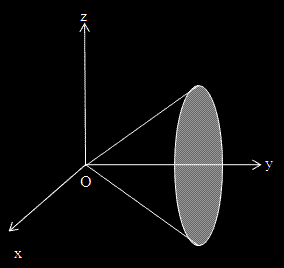
Преминаваме към полярни координати с "основа" равнината Oxz.
x = ρcosφ y = y z = ρsinφ
Якобианът на този преход е ρ.
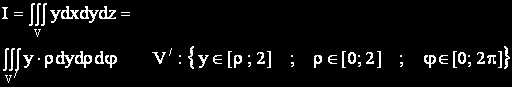
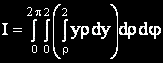
Пресмятаме най-вътрешния интеграл
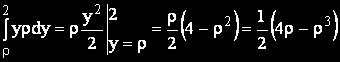
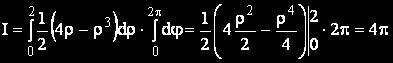
Какво ще научим:
Приложения на тройния интеграл
Теорема на Гаус - Остроградски