Съдържание
Полиноми
Дефиниция
Алгебричен израз от вида:
,
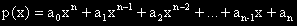където a0 е различно от нула, се нарича полином от n – та степен.
Числата ai , i = 0,1,2...n се наричат негови коефициенти.
a0 се нарича старши коефициент а an – свободен член.
Степента на полинома p(x) се означава с deg ( p(x) ).
За коефициентите ще предполагаме че са цели, рационални числа или реални числа.
Пример: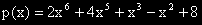 
е полином от шеста степен с коефициенти (2, 4, 0, 1, -1, 0, 8 ).
Старшият коефициент е 2 а свободният член е 8.
Числото a се нарича “ нула” на полинома p(x) ако p(a)=0.
Пример: 2 e “нула” на полинома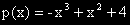 
,
защото:
.
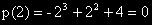Ако a e “нула” на полинома p(x) то p(x) се разлага на множители:
p(x) =(x-a).q(x).
Теорема:Ако p(x) е полином от втора степен, т.е.
p(x)=ax2 + bx +c то p(x) = a.(x-x1). (x-x2) ,
където x1 и x2 са корени на уравнението ax2 + bx +c = 0.
|
Пример: Ще разложим квадратния тричлен 2x2+3x-5 на множители.
Решаваме уравнението:2x2+3x-5=0.
Неговите корени са 1 и -5/2.
Търсеното разлагане е: 2x2+3x-5=0 = 2(x-1)(x+5/2) = (x-1)(2x+5).
Разлагането на един полином на множители улеснява решаването на уравнения и неравенства.
Теорема: Едно произведение е равно на нула тогава и само тогава, когато един от множителите му е нула.
|
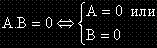
Пример: Ще решим уравнението: (x-2).(3-2x).(2x2 + 3x – 5) = 0.
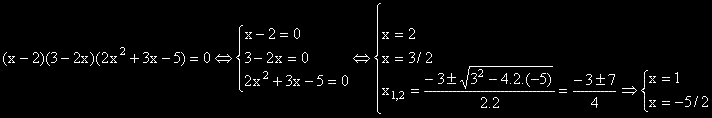
Ще решим неравенството: x3 + x2 - 4x – 4 > 0.
x3 + x2 - 4x – 4 =
x2 ( x + 1) – 4(x +1) =
(x +1)( x2 – 4) = (x +1)(x – 2)(x + 2).
Графиката на функцията y = (x +1)(x – 2)(x + 2) пресича оста Ox в точките –1, 2, -2.
Това са решенията на уравнението y = 0.
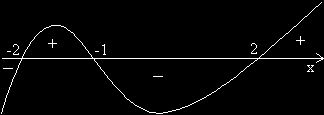
В участъците, в които графиката е над оста Ox е положително, а там, където е под нея – отрицателно.
Това е отразено със знаците + и – над и под абцисната ос.
Решенията на неравенството y>0 са –2 < x < -1 и x>2.
(виж
Метод на интервалите
)
Действия с полиноми
Събирането и изваждането се свеждат до привеждане на подобните членове.
Пример: p(x)= -2x 4 + 3x 2 + 5x + 8,
q(x)= -2x 4 –3x 3 + 4x 2 - x + 3.
p(x)+q(x) = -2x 4 + 3x 2 + 5x + 8 +
(-2x 4 –3x 3 + 4x 2 - x + 3)
= -4x 4 - 3x 3 + 7x 2 + 4x + 11.
p(x)-q(x) = -2x 4 + 3x 2 + 5x + 8 -
(-2x 4 –3x 3 + 4x 2 - x + 3)
= 3x 3 - x 2 +6x + 5.
Тези действия могат да се извършат и като се запишат последователно коефициентите пред подобните
едночлени на полиномите един под друг и се извършат съответните действия.
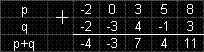
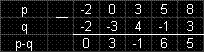
Умният читател, а Вие несъмнено сте такъв, не може да не е забелязал приликата между действията с
полиноми и тези с цели числа. Но умният писател ще Ви увери, че тази прилика не свършва дотук.
Умножението се свежда до разкриване на скоби и привеждане на подобните членове.
Пример: p(x)= 3x2 + x + 8, q(x)= -2x4 –5x3 + 4x2 - x + 3.
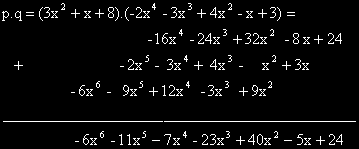
По- разширения запис е предпочетен за удобството подобните членове да попаднат един под друг.
Пропускайки x с неговите степени и използвайки позиционната система, умножението може да се запише така:
Делението на полиноми също прилича много на писменото деление на цели числа.
Но преди това - Теоремата, която е напълно аналогична на тази при целите числа.
Теорема: Ако A(x) и B(x) са полиноми с рационални коефициенти, то съществуват единствени полиноми
Q(x) и R(x), наричани съответно частно и остатък, със следните свойства:
1. A = B.Q + R
2. deg( R ) < deg( B )
|
Намирането на Q и R се извършва по следната схема:
Делят се старшите едночлени на A и B, получава се едночлена q.
Намира се разликата A-B.q и тя заема мястото на A.
С нея се процедира по аналогичен начин докато степента на тази разлика стане по-малка от степента на B.
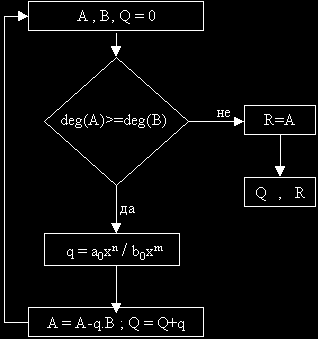
Схемата на последователните действия напомня тази за писменото деление на цели числа, изучавано в училище.
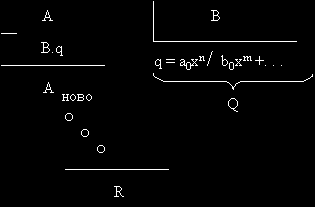
Пример:
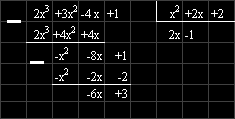
Ето подробностите:
1. Делим старшите едночлени на A и B : 2x3/ x2 = 2x,
което го записваме в мястото на частното.
2. Умножаваме 2x по B и това произведение го изваждаме от A. Разликата е: -x2 - 8x + 1.
С нея постъпваме по същия начин както с A.
3. Делим старшия едночлен на разликата с този на B: -x2 / x2 = -1 ,
което го записваме в мястото на частното.
4. Умножаваме -1 по B и това произведение го изваждаме от -x2 - 8x + 1
Разликата е: - 6x + 3. Нейната степен е по-малка от степента на B. Това е остатъкът.
Разбира се, можем да използваме позиционирането, пропускайки променливата с нейните степени и използвайки само коефициентите, съобразявайки се с тяхната позиция.
Тогава горното деление ще придобие вида:
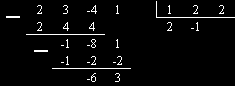
Какво ще научим:
Схема на Хорнер
Съдържание