Какво трябва да знаем:
Полиноми

Схема на Хорнер

Теорема: ( Безу ) Нека p(x) е полином и a е произволно число. Тогава остатъкът при деление на p(x) на полинома от първа степен (x-a) е числото p(a) - стойността на полинома p(x) при x = a.

Делението на полинома p(x) на x-a се извършва по Схемата на Хорнер.
Записват се коефициентите на полинома p(x) а вдясно и по-долу числото a.
Под тях се получават коефициентите на частното а най-накрая остатъкът при това деление - r,
което според теоремата е равно на p(a).

Работи се по следната схема:

Графика на y=(x+1)(x– 2)(x+2)

b₀ = a₀ .
Всяко следващо b_k е равно на a по предходното b_k-1, плюс следващото a_k.
b_k = a.b_k-1 + a_k .
Така се получава и r.

Ето повече детайли:

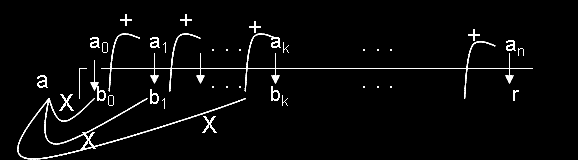
b₀ = a₀ b₁ = a.b₀ + a₁ b₂ = a.b₁ + a₂ .......................... b_k = a.b_k-1 + a_k .......................... b_n-1 = a.b_n-2 + a_n-1 b_n = r = a.b_n-1+ a_n

Пример: Ще намерим частното и остатъка при делението на полинома p(x) = 2x⁴ -3x² + 3 с x-2.
Коефициентите на p(x) са: (2,0,-3,0,1). Прилагаме схемата на Хорнер.

Коефициентите на частното са: (2,4,5,10).
Следователно то е: Q(x) = 2x³ +4x² + 5x+10. Остатъкът е R = 23.
Това число е стойността на p(x) при x = 2.
Действително: p(2) = 2.2⁴ -3.2² + 3 = 23.

Пример: Ще намерим частното и остатъка при делението на същия полином p(x) с x + 2.
Схемата на Хорнер се прилага при деление на полином от вида x-a.
x+2 = x-(-2), затова вдясно трябва да поставим числото -2.

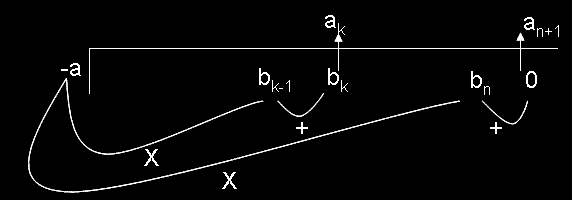
Задача: Може ли да се използва подобна схема за умножаване на полином p(x) по полином от вида x-a ?
Отговор: Може:

Теорема (Гаус): Нека p(x) = a₀xⁿ + a₁x^n-1 + ..... + a_n-1x + a_n e полином от n-та степен с цели коефициенти. Ако a = p/q е рационален корен на уравнението: p(x)=0 , то p е делител на a_n и q е делител на a₀ .

Съдържание