Съдържание
Метод на интервалите
Този метод се използва за решаване на неравенства от вида:
(x – x1)( x – x2)…. ( x – xn-1) ( x – xn) >0.
Ще предполагаме, че x1 , x2 … xn-1 , xn са различни числа и
x1 > x2 > x3 >.... > xn-1 > xn .
Графиката на функцията
y = (x – x1)( x – x2)…. ( x – xn-1) ( x – xn)
има вида посочен на чертежа:
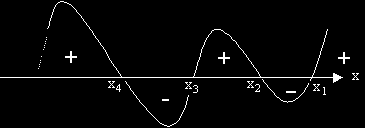
Тя пресича оста Ox в точките и с абциси: x1 , x2 , x3 … xn .
Това са решенията на уравнението y = 0.
В участъците, в които графиката е над оста Ox y е положително, а там, където е под нея – отрицателно.
Това е отразено със знаците + и – над и под абцисната ос.
Решенията на неравенството y>0 са интервалите от абцисата, при които знакът е плюс.
Пример
Съдържание