Леки промени под знака на диференциала
От формулата dF(x)=F'(x) следва, че:

Под знака на диференциала можем да прибавяме произволна константа.
Ако умножим под знака на диференциала, с константа, трябва и да разделим на нея.
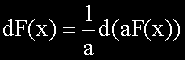
Двете формули можем да обобщим с формулата:
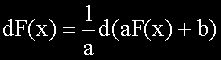
Тази формула, съчетана с формулата за сложен интеграл ни дава възможност да направим
съществено разширяване на табличните интеграли по следната схема чрез дедукция
( дедукцията е начин на разсъждение от общото към частното, противоположен на индукцията ).

Ето примери с конкретна подинтегрална функция.
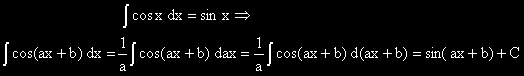
Тук се наблюдават основните елементи на преобразуванията под знака на диференциала -
умножаване по a и делене на a.
Прибавянето на константа b, без да има нужда от нейното изваждане и накрая
прилагането на формулата
за сложен интеграл.
Аналогично:


Пресметнете интеграла:
Решение:

Пресметнете интеграла: 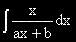
Решение:
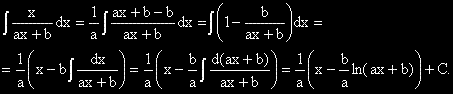
Ще използваме тригонометричните формули за намаляване на степента: ,
,
за пресмятане на интегралите: 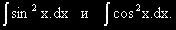

Какво ще научим:
Внасяне под знака на диференциала