Функции с реален аргумент и комплексна стойност
Планетарен пример
Страницата е свободен превод от книгата
"Комплексен анализ" автор Джордж Кейн
Със знаците * и + са означени началото и края на коментарите,
които преводачът си е позволил.
Да предположим, че е дадено тяло с маса M, фиксирано в началото на координатната
система - като Слънцето и друго тяло, свободно в своето движение с маса m - като планета.
Нека положението на второто тяло във време t е зададено с функция z(t) с
комплексни стойности.
Предполагаме, че единствената сила, действаща на второто тяло е гравитационната,
предизвикана от фиксираното тяло.
Така, че тази сила - f е:
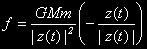
където G е универсалната гравитационна константа.
Сър Исак Нютон ни казва, че
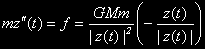
Следователно,
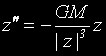
Нека по-нататък да напишем това в полярни координати: z = r.ei.φ :
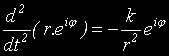
където положихме k: = G.M. Да видим какво се получи.
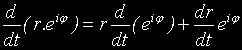
Сега:
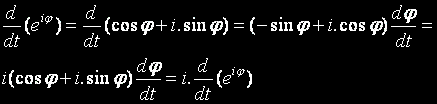
Така, че:
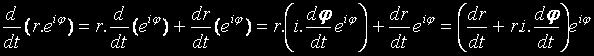
Сега:
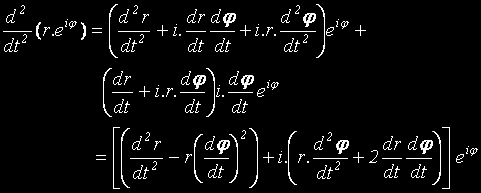
Сега равенството
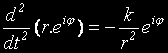
придобива вида:
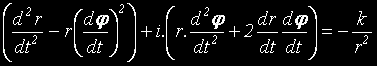
Това ни дава две уравнения:
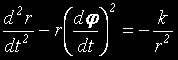
и
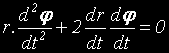
Умножавайки по r, от второто уравнение получаваме:
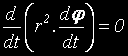
Това ни показва, че:
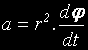е константа.
(Тази константа се нарича ъглов момент * или площна скорост +.)
Този резултат ни позволява да се освободим от
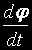в първото от по-горните, две уравнения:
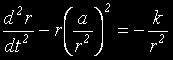
или,
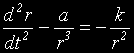
Въпреки, че уравнението сега включва само една неизвестна функция,
както стои е трудно за решаване.
Да сменим променливите и да мислим за r като
за функция от φ.
Нека също запишем нещата чрез
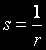
Тогава:
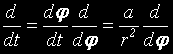
* Тук се има предвид диференциране на произволна функция, чийто символ е пропуснат.
Подобни означения са характерни за операторите. +
Следователно,
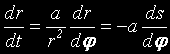
и така
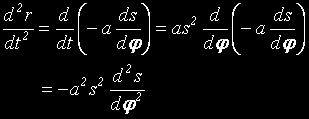
и нашето диференциално уравнение придобива вида:
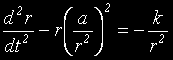
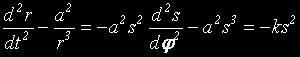
или:
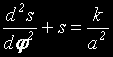
Това е лесно за решаване. От гимназиалния курс по
диференциални уравнения, си спомняме, че:
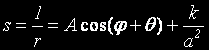
където A и θ са константи, зависещи само от началните условия.
И най после:
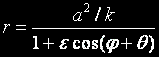
където положихме
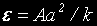
Графиката на тази функция е, разбира се, конично сечение с екцентритет ε.