Какво трябва да знаем?
Тест на Уилкоксън-Ман-Уитни или тест с ранжирани суми
Условия за прилагане на теста
Нека са зададени две непрекъснати и независими генерални съвкупности
X1 и X2 със средни стойности
μ1 и μ2 , които не са непременно нормално разпределени, както се изисква при t-теста.
Да предположим, че X1 и X2 имат еднакви по форма графики на плътността на
разпределение и се различават единствено по своето положение.
[1]D:\Stancho\Books\Math\Math1\Probability and statistics\Statistics\En\Applied
Statistics And Probability For Engineers - Montgomery && Runger
page 702
Тук читателят може да се запознае с по-слаби изисквания.
?
Издигаме нулевата хипотеза
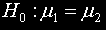и нейната алтернативна хипотеза:
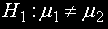
Нулевата хипотеза е равенството на средните на две генералнати съвкупности при извадки с обеми
n1 и n2 , като предполагаме, че
.
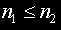Наблюдаваните стойности на случайната величина се подреждат във възходящ ред като на всяка от тях се съпоставя пореден номер.
Ако има няколко повтарящи се стойности номерата, които им се съпоставят са едни и същи и са равни на средно-аритметичното
на поредните им номера.
Пример
?
Да означим с N общия брой от двете извадки: N = n1 + n2 .
Нека W1 и W2 са сумите от ранговете на първата и втората извадки.
В сила е равенството
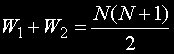
Статистиките в случая са две - W1 и W2 .
Ако нулевата хипотеза е вярна - т.е. ако липсва разлика между средните на двете извадки, то
W1 и W2 са приблизително равни на N(N+1)/2 .
Двете статитики се сравняват с критичната стойност
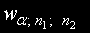, зададена в таблиците при дадени n1 и n2 е зададена степен на значимост μ.
Нулевата хипотеза
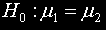се отхвърля в полза на алтернативната
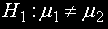, ако една от двете стойности - W1 и W2 е по-малка или равна на критичната.
Описаната процедура може да се използва и за едностранна алтернатива.
Ако алтернативната хипотеза е от вида
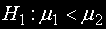нулевата хипотеза се отхвърля ако
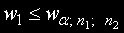
Ако алтернативната хипотеза е от вида
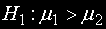нулевата хипотеза се отхвърля при
.
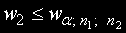Пример
Изследваме две сплави, предназначени за изработка детайли за самолет за издържливост на опън.
Първата сплав е общоприетата а втората е новата - алуминиево-литиева сплав е много по-лека от обикновения материал.
Експериментът е проведен върху 10 образци от всяка сплав и резултатите от него са представени в две таблици - за първата
и за втората
сплав в мерна единица килопаскал.
Подреждаме измерванията в колона, като в допълнителна - първа графа отбелязваме номера на сплавта:
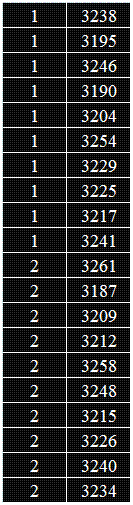
Подреждаме стойностите в нарастващ ред, като в допълнителна - трета графа записваме поредния номер:
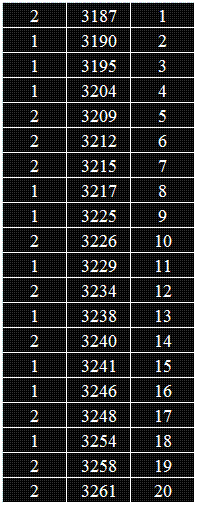Събираме номерата, съответстващи на първата сплав и тези на втората, за да получим
W1 и W2 .
?
Получаваме W1 = 99 и W2 = 111.
При избраното ниво на значимост α = 0,05 и при обеми на извадките
n1 и n2 определяме критичната стойност
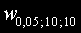от
таблицата .
Тя е
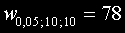
Понеже изчислената статистиката е по-голяма от критичната стойност
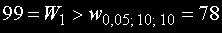нулевата хипотеза не може да бъде отхвърлена.
Ако n1 > 8 и n2 > 8 разпределението е приблизително нормално със
средна стойност n1(N+1)/2 и дисперсия n1n2(N+1)/12.
В горния пример може да се приложи и приближението с нормалното разпределение.
Определяме средната стойност на величината W1 по формулата:
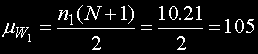Определяме и стандартното отклонение по формулата
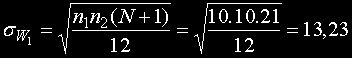
Получаваме тестовата статистика
.
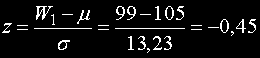Понеже критичната стойност при избраното ниво на значимост е -1,64 то нулевата хипотеза не може да бъде отхвърлена.
Таблица с критичните стойности за теста на Уилкоксън-Ман-Уитни или тест с ранжирани суми.
?
Какво ще научим: