Сър Роналд Фишер, тест за хомогенност на генералните съвкупности и българската домашна сланина
Българинът си яде сланинката, пуши си цигарката ...
Министър-председателят Бойко Борисов за здравето на народа
Пред двадесетте години на XX век
Сър Роналд Фишер
Роден 17 февруари 1890 г. Лондон, Великобритания - Починал 29 юли 1962 г. (72 г.) Аделаида, Австралия
е предизвикал революция в статитиката, проверявайки и осмисляйки направеното дотогава.
Но той е открил и нови подходи към статитическите изследвания като анализ на вариацията, степените на свобода, факторния анализ и
ги е обединил в едно цяло. Разпръснатите знания по статистика, откривани и осмисляни в продължение на 200 години са кристализилали в
неговите изследвания в професионални методи, които днес ние изучаваме и използваме.
Фишер е осъзнал, че методът на оценка само на една генерална съвкупност, използвайки извадка с голям обем е метод, несъответстващ
на тогавашните изисквания.
Назряла е необходимостта от съвременни средства и методи на статистическите средства за изследване на явленията и
влияещите им фактори.
Това е обективната причина за появата на две нови статистически методики - χ2
(хи-квадрат) -тестовете и анализа на вариацията.
Първата статия за χ2 -тестовете е публикувана през 1900 г. в непретенционно списание и въпреки това методиките,
описани в нея не само са оцелели през годините, но и са претърпели главозамайващо развитие в използването им в производството,
науката и неплановия пазар.
В голяма степен χ2 -тестовете си приличат.
Данните се нанасят в таблица на емперичните (наблюдаваните) честоти, която се нарича таблица на спрегнатост.
По нея се определят теоретичните честоти и степента на различие между едните и другите.
Целта на теста е да се определи, подобно на регресионно-корелационните изследвания степента на зависимост в която
единия фактор (променлива) се влияе от другия.
Вьпреки приликата, χ2 тестовете се различават в тьлкуването на резултатите.
Някои оценяват независимостта на две величини от една генерална съвкупност, други хомогенността на няколко генерални
съвкупности (като под хомогенност се разбира еднаквостта на отношението на видовете в различните генерални съвкупности),
трети степента на доближаването (пасването на емпиричните (наблюдаваните) честоти с теоретичните.
Макар, че изследванията на пазара датират от края на XIX в. те не са били повече от информация
за вкусовете на купувачите.
Истинското приложение на статистиката в меркантилните проучвания е започнало през 30-те години на XX век.
В голяма степен научния подход се дьлжи на успехите на статистическата методология, основана на новите извадкови операции,
разработени от сьр Роналд Фишер.
Но (и това е може би по правдоподобно) и на тежкото икономическо положение по това време.
Компаниите са били принудени от Голямата Депресия да използуват науката за да изльжат потребителите да купуват.
Детайл от картината на Еронимус Бош "Корабът на глупците"
Така се е появила ерата на маркетинга.
Ще разледаме, заедно, пример от нашата нерадостна действителност.
Производителите на домашна, българска сланина поръчват на българските статистици статистическо изследване вьрху
нагласите на потребителите по отношение на произвеждания от тях продукт - домашна ,бьлгарска сланина.
Целта на изследването е да се отговори на въпроса:
"Съществува ли различие по отношение на продукта при три групи потребители, определени от поръчителите?
Ако такова съществува до каква степен може да му се доверим?"
Генералните сьвкупности са три - група А, група Б и трета група,сьстояща се единствено от Бойко Борисов.
От тях са извлечени извадки с различни обеми, които при нашето проучване не са взети предвид.
Поради особеностите на извадките, особено третата, резултатите били отчитани в проценти (%).
Ние - изследователите издигаме нулевата хипотеза
H0 - "Групите са хомогенни в предпочитанията си към продукта."
Противоположната хипотеза е H1 - " Групите не са хомогенни в предпочитанията си към продукта."
Избира се степен на достоверност е α=0,005.
Ако нулевата хипотеза бъде отхвърлена то противоположната ще бъде вярна в
1- α = 1-0,005 = 0,995 = 99,5% от случаите.
Процентите за пьрвите две извадки, те са нанесени в таблицата:
| |
А |
Б |
| Обичат сланина |
10 |
60 |
| Не обичат сланина |
80 |
20 |
| Нито едното, нито другото |
10 |
20 |
При проучване на третата група се оказало,че сьщността на Б.Б. е разделена,по отношение на сланината "пийсе на пийсе".
Ето крайните резултати,получени от анкетираните:
| |
А |
Б |
Бойко Борисов |
| Обичат сланина | 10 | 60 | 50 |
| Не обичат сланина |
80 | 20 | 50 |
| Нито едното, нито другото |
10 | 20 | 0 |
Стойностите в таблицата се наричат "наблюдавани" или "емпирични честоти".
Ще ги означаваме с Fij , където i е номерът на реда а j - номерът на колоната.
Броят на редовете ще означим с r а този на стълбовете със c.
След това в таблицата се нанасят сумите по редове и колони
Тези суми ще означаваме с Ri и Cj .
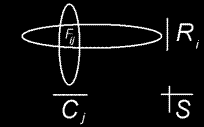Общата сума на наблюдаваните (емпиричните) честоти ще означим със S.
| |
Група А |
Група Б |
Бойко Борисов |
Сума |
| Обичат сланина |
10 | 60 | 50 | 120 |
| Не обичат сланина |
80 | 50 | 50 | 150 |
| Нито едното, нито другото |
10 | 20 | 0 | 30 |
| Сума |
100 | 100 | 100 | 300 |
След това, за всяка клетка се изчисляват теоретичните честоти по формулата
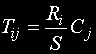Te се нанасят в таблицата вдясно и над наблюдаваните честоти:
| |
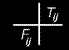
Група А |
Група Б |
Бойко Борисов |
Сума |
| Обичат сланина |
|
|
|
120 |
| Не обичат сланина |
|
|
|
150 |
| Нито едното, нито другото |
|
|
|
30 |
| Сума | 100 | 100 | 100 | 300 |
По-нататък се определят събираемите за всяка клетка, необходими за изчисляването на статистиката χ2.
Те се изчисляват по формулата
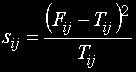където Fij е наблюдаваната честота
Tij теоретичната честота
Sij е изчисляваното събираемо и се нанасят под Tij и вляво на Fij.
| |
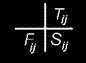
Група А |
Група Б |
Бойко Борисов |
Сума |
| Обичат сланина |
|
|
|
120 |
| Не обичат сланина |
|
|
|
150 |
| Нито едното, нито другото |
|
|
|
30 |
| Сума |
100 | 100 | 100 | 300 |
Статистиката χ2 се изчислява като сума от деветте събереми Sij (тези в червените полета):
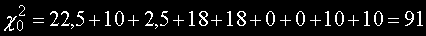Броят на степените на свобода f е равен на произведението f = (r-1)(c-1) където c е
броят на колоните а r - този на редовете. В нашия случай f = 4.
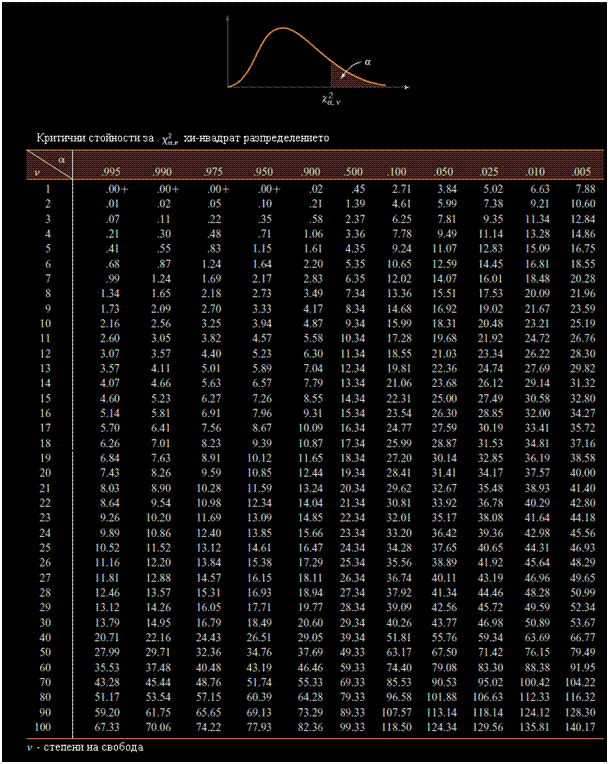
От таблицата на критичните стойности за χ2-разпределението намираме, че при избраната степен на
доверителност α=0,005 и при четири степени на свобода
.
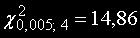Тогава
.
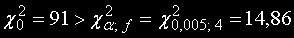При изпълнение на такова неравенство Ние, статистиците, смело отхвърляме нулевата хипотеза.
Нехомогенността на трите групи се дължи на тяхната специфичност, особено на третата, чийто единствен член ярко се отличава
от останалия "матриял".
Таблица на критичните стойности на χ2-разпределението
