Аналитично условие точката X (x, y) да е вътрешна за отсечката [AB]

Какво трябва да знаем:
Уравнение на права през две точки
Деление на отсечка в дадено отношение 		Приложение на производните

Теорема:

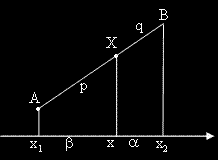
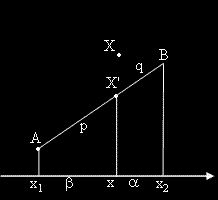
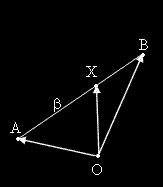
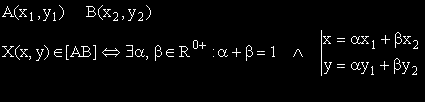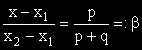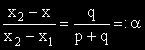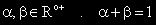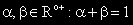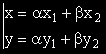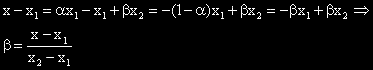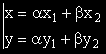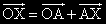В равнината са зададени две точки A и B със своите координати A(x1 , y1 ) и B(x2 , y2 ) .
Необходимо и достатъчно условие точката X (x, y) да е вътрешна за отсечката [AB] е
съществуването на две неотрицателни числа α и β със сума единица, за които е изпълнено:
.

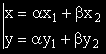Ето и символичният запис на теоремата:

Доказателство:
Необходимост ( Þ )
Нека точката X(x,y) принадлежи на отсечката AB.
Да означим дължините на отсечките AX и XB съответно с p и q.
Проектирайки точките A, X и B върху оста Ox от теоремата на Талес, получаваме отношенията:


Ясно е , че a и b са неотрицателни числа със сума единица.
Достатъчност ( Ü )
Точка X е с координати (x, y) за които съществуват , такива, че:
Да извадим от двете страни на първото уравнение x1 .


От необходимостта следва, че координатите на точка X' от отсечката AB, са:

Следователно двете точки съвпадат X и X '.

Другото доказателство показва преимуществата на използването на векторите.


Но векторът AX е колинеарен и еднопосочен на AB.
Тогава AX = β . AB, където b Î [0, 1]
Получаваме OX=OA+b.(OB - OA) = (1-b) . OA+b . OB.
Да положим 1-b = a
Записвайки това по координати получаваме желаното равенство.

Нали така?!