Какво трябва да знаем:
Извода на каноничните уравнения на елипсата
Допирателни към крива
Аналитична геометрия

Есцентритет, директриса и допирателни


Предполагаме, че познаваме дефинициите на коничните сечения и
изводите на техните канонични уравнения в декартова координатна система.
Да си припомним
а - дължина на голямата полуос
b - дължина на малката полуос
Естествено 2a и 2b са дължините на голямата и малка ос.
По нататък, единствените параметри, които ще считаме за известни са a и b.

Разстоянието между фокусите на коничното сечение се нарича междуфокусно разстояние.

Чертеж 1

Изразете го чрез a и b.
Намерете координатите на фокусите на елипсата?
Чертеж 2draft2

Formula 1

Междуфокусното разстояние се означава с 2c
В сила е равенството a2 + b2 = c2.

Фокална хорда се нарича хорда на конусно сечение, прекарана през единия от фокусите му.
Дължината на перпендикуляра, издигнат от фокуса F1 до пресечната му точка с
елипсата се нарича фокален параметър.
Означава се с p и е равен на p = b2/a.
Чертеж 3


Formula 2

Архимед е доказал, че отношението на ординатите на елипсата и
описаната около нея окръжност е постоянно и е равно на b/a.
Чертеж 4


Formula 3

От характеристичното свойство на елипсата ρ1 + ρ2 = 2a ,
следва, че съществува такава функция ε(x) , за която
ρ1 = a + ε(x) и ρ2 = a - ε(x).

Оказва се, че ε(x) = (a/c)x.
Чертеж 5

Formula 4
Formula 5

Отношението Formula 6 се нарича ексцентритет.

Правата с уравнение x = a/ε се нарича директриса на елипсата с уравнение относно левия фокус F1.
За всяка точка A от елипсата отношението на дължините на фокалния радиус ρ1 и
разстоянието r до директрисата е равно на ексцентритета ε .


Чертеж 7


, както знаем.
Ясно!

Уравнението на допирателната към елипсата през точка A(x0 , y0 ), лежаща на нея е:
Чертеж 8

Formula 11


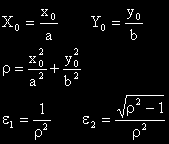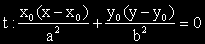
Поради това, че точка A е от елипсата горното уравнение може да се запише така:
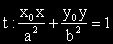
Formula 11

Ако точка A е точка от елипсата отсечките F1A и F2A се наричат фокални радиуси на точката A.
Фокалните радиуси в точка А от елипсата сключват равни ъгли с допирателната, прекарана през А.

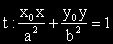
Уравнението на допирателната през A(x0 , y0 ) е Formula 11
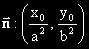
Векторът Formula 14 е перпендикулярен на t.
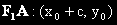
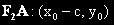
Векторът Formula 15_1 е по единия фокален радиус а Formula 15_2 по другия.
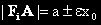
Техните дължини са Formula 16
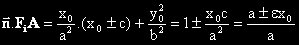
Formula 17
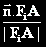
Formula 18 не зависи от i, което доказва твърдението.
Чертеж 9

Допирните точки на допирателите към елипсата, прекарани през точка A(x0 , y0 ), нележаща на нея имат координати:

Formula 32,
където:
Formula 33


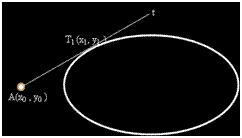
Чертеж 10

Нека T1 е допирната точка.
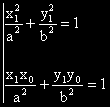
Тогава: Formula 19
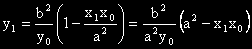
Изразяваме y1 от линейното уравнение Formula 21
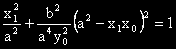
Заместваме го в първото: Formula 22
Подреждаме по степените на неизвестното x1 в полученото квадратно уравнение.
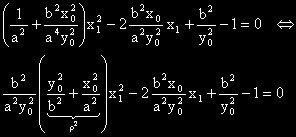
Formula 23
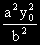
Умножаваме по Formula 24 за да се освободим от знаменателя.
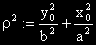
Полагаме Formula 25
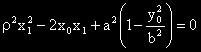
Получаваме: Formula 26
Намираме дискриминантата на полученото квадратно уравнение.
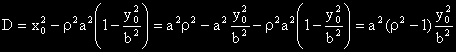
Formula 27
Ще решим кватратно уравнение, въвеждайки подходящи означения.
С x1,2 означаваме абцисите на допирните точки T1 и T2 .
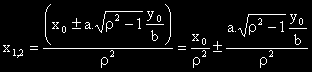
Formula 28
Означаваме с Formula 29
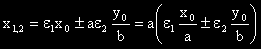
Получаваме: Formula 30
Сега ще намерим y1,2 .
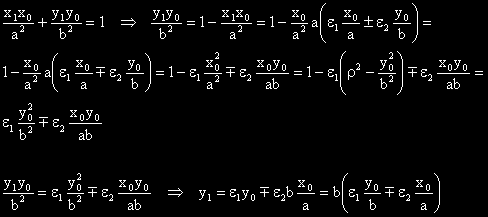
Formula 31
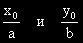
Константите Formula 31_1 означаваме с X0 и Y0.
Получихме, че:
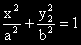
Ако е дадена елипса с уравнение Formula 0 към която са прекарани двете допирателни през точката A(x0 , y0 ) то
допирните им точки с елипсата имат координати
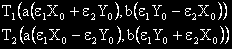
Formula 32
където:
Formula 33


Какво ще научим:

Полюс на права спрямо елипса