Хераклит (540-480 г пр н е)е твърдял, че не може човек да влезе два пъти в една река, защото водата, която го е обливала първият път е различна от тази във втория.
Но ако той плува с лодка водата остава същата, но тогава човекът не може да слезе два пъти на един и същи бряг.
Но има неща, които свързват реката със брега. Времето със Съвремието.
Разказът е за една вечна Книга. Заглавието и е „Начала” или латинизирано „Елементи”.
Написана е от Евклид (IV-III в. пр. н. е.).
Оскъдните сведения за него се изчерпват с това, че е
преподавал в Александрия – Египет по времето на Птолемей I Сотер (спасител 367-283 пр. н. е. ).
Известни са два анекдота за него, написании от Прокъл (410-485 г) -хронограф на науката, живял
във Византия.
Веднъж цар Птолемей го попитал няма ли по-лесен начин за изучаване на геометрията, освен този,
изложен в „Началата”, на което Евклид отговорил:
„В геометрията царски пътища няма.”
И другият:
Един ученик попитал Евклид каква е ползата от цялото това Учение.
Учителят казал на слугата си:
„ Дай му три обола (пари), защото той иска да спечели от своето учене.”
Евклид се е държал дружелюбно с учениците си и особено е ценял тези, които са проявявали усърдие в учението.
Книгата се е запазила по чудо в превратностите на историята. Други антични съчинения са имали
по-нещастна съдба и за тях се знае само по коментари.
Александрийската библиотека, събрала цялата антична памет е горяла няколко пъти. Писано е че
последния път жителите на града половин година са използвали ръкописите по най-пълноценен
начин – в печките.
Не е ясно до каква степен Евклид е автор на предложенията (теоремите) и на доказателствата изложени в Книгата. В много от случаите той не е но не заявява авторството. Това вероятно е така, защото Евклид е желаел да изложи Геометрията а не нейната История.
Книга V е посветена на пропорциите. Това учение е систематизирано от Евдокс (408-355 пр.н.е.) Роден е в град в Мала Азия. Учил е медицина в Сицилия. На 20 г пристигнал в Атина, привлечен от основаната от Платон (427-347 пр.н.е.) Академия. Евдокс е откривателят на метода на изчерпването – метод за изчисляване на лица и обеми ограничени от криви линии и повърхнини.
Но още по-рано, в VI в пр. н. е. , Питагор (540-490 пр. н. е. ) основава школа в гръцката колония в южна Италия – гр Кротон. Дейността на членовете и била забулена в тайна за непосветените. Питагорейците наричали своето учение „Математа” което означавало наука или знание. То се състояло от четири части: Аритметика, Геометрия, Астрономия и Хармония. Последната, касаеща изкуствата, е била най-висшата но дори и тя имала за основа Аритметиката – наука за числата и техните отношения. Планетите обикаляли Земята издавайки чудни звуци но хората нямали способността да им се наслаждават поради своята суета. Тази небесна музика била достъпна само за Питагор. Според византийският историк Прокъл именно Питагорейците са открили петте платонови тела тераедър, куб,октаедър, икосаедър (двадесетостен) додекаедър ( дванадесетостен )
В космогонията на Питагорейците цялото число е същността на предмета ( тялото, единицата битие)
а отношението между предметите се изразяват чрез отношение между представящете ги числа.
Но самите Питагорейци са открили, че числото
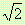не може да се изрази като отношение на цели числа.
Според писмено сведение, един ученик - Хипас издал тайната на непосветените. Питагорейците го
прокълнали и му направили преживе гроб, желаейки да му навредят.
Теетет Атински е ученик на питагорееца Теодор и Платон. Теетет загинал млад. През 369г пр. н. е. е
смъртно ранен в Коринтската битка. Умиращият герой е бил откаран в Атина, където е починал. Погребан е
с почести.
Имал е изпъкнали очи и чип нос но се е отличавал с необикновена доброта и ум. Платон му е предричал
напредък в добродетелите и му е посветил един от своите „Диалози”.
Последните три части на Книгата са посветени на откритията, направени от Теетет.
Но основното в Книгата не са фактите а последователността на тяхното изложение и начина на аргументация
(доказателството). При доказване на едно твърдение се използват вече доказани твърдения. Този метод на
доказателство се нарича дедуктивен. Има и други методи на аргументация – индуктивен, по аналогия или
дори „Някъде пише, че …”.
Един математик-историк пише, че за много науки не е известно кога са възникнали но за Математиката е
известна дори точната дата. Той цитира едно писмо от Талес Милетски (625 – 547г пр н е ), в което
той обосновава твърдението, че диаметърът се вижда от всяка точка на полуокръжността под прав ъгъл.
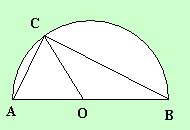
Талес използва твърденията:
1.Ъглите при основата на равнобедрен триъгълник са равни.
2.Сумата от ъглите на всеки триъгълник е равна на два прави ъгъла (1800 ).
Той се гордее от това, че макар и този факт да е известен на всеки „строителен инженер на пирамиди”
в Египет, никой от тях не може да го обоснове. Талес е доказал I и II признак на еднаквост на
триъгълници.
Всеки ученик учейки и всеки учител преподавайки му отдаваме почит изучавайки
„Теоремата на Талес”.
През 585г пр. н. е. той е предсказал слънчево затъмнение, по свидетелство на Херодот -
Бащата на историята.
Такива са били авторите.
Но Книгата има още един автор - Времето, реката, в която се влиза само веднъж.
За девет години (332- 323г. пр.н.е.) Александър Македонски покорил Гърция, Персия, Бактрия и част от
Индия - разпространявайки елинската култура в целия античен свят. Краят на тази, т. н. Елинистична
епоха настъпва през 30 г. пр. н. е. със завладяването на Египет от римляните.
Александър е основал в Египет град, и с типична за него скромност го е нарекъл Александрия.
След неговата смърт пълководците са разделили помежду си завоюваните страни. В Египет е основана
династията на Птолемеите. Последният и представител била красивата Клеопатра. А първият -
Птолемей I Сотер избрал за столица на Египет Александрия 1.
Там (написано е "там" а не "тук", защото тук такива неща не стават) той основал храм на музите -
Музейон, част от който била
Александрийската библиотека. Тя наброявала 700 000 тома (свитъци). Основата и била положена
от личната библиотека на Аристотел.
Там е бил Евклид - сред музите. Там е написал Книгата.
Общественото устройство в Гърция е било робовладелско. С философия, изкуства и математика са се
занимавали Свободни граждани. Те не са били заети със занаятчийство и рядко с търговия.
Платон е устоявал мнение, че професията "търговец в лавка" е недостойна за Свободен гражданин и
тези, които унижавали свободата по този начин да бъдат третирани като престъпници.
Беотийците (гражданите от областта Беотия) лишавали гражданите, "изцапали" ръцете си с пари от
търговска сделка, от правото да заемат обществени длъжности.
Такова е било Времето.
1. Точката е това, което няма части.
2. Линията – това е дължина без ширина.
3. Права линия е такава, която е еднакво разположена по отношение на точките върху нея.
Дефинират се повърхнина, равнина, ъгъл- прав, тъп и остър. Въвежда се кръгът със своите елементи.
Систематизират се видовете триъгълници и четириъгълници.
…………………………………………….
23. Успоредни са такива прави, които се намират в една и съща равнина и при неограничено
продължаване в двете им страни не се срещат помежду си нито от едната, нито от другата страна.
Следват пет постулата, обясняващи кои са позволените построения.
Иска се:
(1) От всяка точка до всяка точка да може да се прекара права.
(2) И от всеки център, със всеки разтвор да може да се опише кръг.
………………………………………….
(5) И ако права, която пада върху две прави, образува вътрешни ъгли, които лежат от едната и
страна и са по.малки от две прави, тези прави, продължени неограничено, да се срещнат от онази страна,
в която ъглите са по малко от два прави.
Девет аксиоми определят правилата за обосновка.
1) Равните на едно и също са равни помежду си.
………………………………
7) И покриващите се едно с друго са равни помежду си.
8) И цялото е по голямо от частта си.
9) И две прави не съдържат пространство
Следват 13-те части на Книгата:
I. Свойства на триъгълниците. Признаци на еднаквост. Построяване на бисектриса, среда на отсечка и перпендикуляр към права. Изчисляване на лица. В тази част се въвеждат свойствата на успоредните прави. Тази част завършва с Питагоровата теорема.
II. В тази част са положени основите на т.н. геометрична алгебра, произхождаща още от Питагор. Величините тук не са разгледани като числа, а като дължини и лица на геометрични фигури.
III Геометрия на окръжността.
IV Правилни многоъгълници. Вписани и описани многоъгълници.
V Посветена е на свойствата на пропорциите и се отличава с висок стил.
VI Подобност на фигури и приложението на лицата им.
VII , VIII и IX част са посветени на свойствата на целите числа и на техните отношения. По същество в тях е изложена теорията на рационалните числа. Тук е доказана теоремата за съществуването на безбройно много прости числа.
X разглежда ирационалните числа.
XI Стереометрия.
XII Изчисляват се лицата на криволинейни фигури чрез използване на метода на изчерпването открит и използван за същата цел от Евдокс.
XIII Построяват се петте Платонови тела.
Книгата завършва без послеслов.
Евклид плува в реката на времето а мостът, свързващ неговият кораб
с брега се е превърнал в тънка нишка под формата на книга.
И когато човек се загледа внимателно в нея ще прочете:
„ От всяка точка до всяка точка се иска да се прекара права”.
1 Причините за упадъка на Елинизма са завладяването на Гърция от Рим и Християнството, провъзгласено
от Константин Велики през 313г за официална религия в Римската империя.
Теодосий (375-392 г. ) забранява езическите религии.
В 529г византийският император Юстиян заповядва да се закрие Платоновата Академия, просъществувала 800
години.
През 47г. пр. н. е. римляните опожарили Египетския флот в александрийското пристанище. Пожарът
обхванал и града. Унищожена е и Александрийската библиотека.
В годината, когато Теодосий забранява езическите религии християните разрушили храма на Серапеис -
Серапейон - хранилище на уникални гръцки ръкописи.
Египет е завладян от арабите през 640г. Всички оцелели книги са били унищожени.
Преданието говори, че халиф Омар обосновал необходимостта от това с думите:
"Ако тези книги повтарят написаното в Корана, то ненужно е да се четат. Ако му противоречат - не
трябва да се четат.".