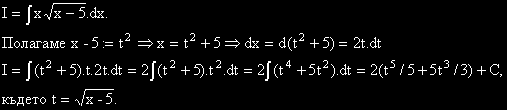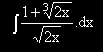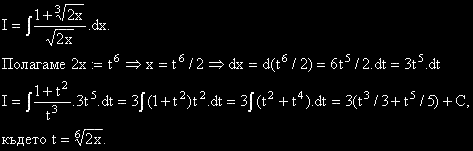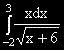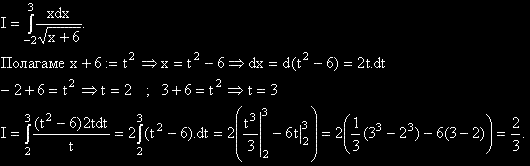Решения на типични изпитни задачи

1. Аналитична геометрия
Задача 1 Задача 2 Задача 3
2. Транспортна задача
Задача 1 Задача 2
3. Частни производни
Задача 1
4. Екстремуми на функция две променливи
Задача 1 Задача 2
5. Интеграли
Задача 1 Задача 2 Задача 3
6. Вероятности
Задача 1 Задача 2 Задача 3

Аналитична геометрия

• Задача 1 Начало

Триъгълник има връх с координати (-4,-5) и височина, лежаща върху правата с уравнение: 5x+4y=0.
Да се намери уравнението на една от страните на триъгълника.
Решение:

Точка А не принадлежи на правата h:5x+4y=0, защото нейните координати не удовлетворяват нейното уравнение. kh = -5/4. h ^ AB Þ kh . kAB = -1       Þ kAB = 4/5 Следователно: AB: (y- (-5) ) = 4/5.(x- (-4) ) Û AB: y = 4x / 5 -9 / 5 .

• Задача 2 Начало

Даден е триъгълник с върхове A(3,2) , B(-1,-1) и C(11,6). Точките M и N са среди съответно на страните AB и AC.
Да се напишат уравненията на правите BC и MN и да се пресметне дължината на отсечката MN.
Решение:
• Задача 3 Начало

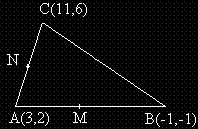
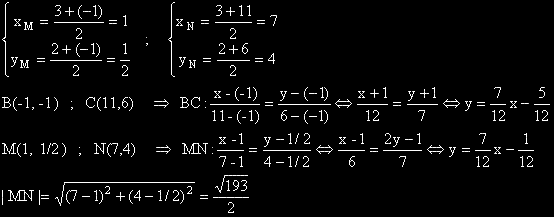
Да се напише общото уравнение на права минаваща през точка с координати (2 ,1) и през пресечната точка на правите с уравнения: 3x - 2y + 1=0 и x - y + 1=0.

Решение:

Транспортна задача

• Задача 1 Начало

Намерете оптималните транспортни разходи за транспортната задача:


Решение:

Попълваме на началния план по метода на минималните транспортни разходи.




За запълнените клетки определяме потенциалите така, че сумата им да бъде равна на транспортните разходи за всяка запълнена клетка. Т.е. ui + vj = tij за всяка пълна клетка. За u1 даваме произволна стойност, например 3 .




Определяме оценките D ij = ui + vj - tij за свободните клетки. D 12= 3 + 13 - 28<0 ; D 23 = -12 + 2 - 25<0 ; D 24 = -12 + 0 - 15<0 ; D 31 = -1 + 14 - 16<0 ; D 32 = -1 + 13 -3 = 9>0 ; D 34 = -1 + 0 - 12<0

Клетката (3,2) е единствената клетка с положителна оценка. Построяваме цикъл с начало тази клетка, и запълнени останали върхови клетки.
Започвайки от изходната, поставяме знаци + и - на върховете на цикъла.

Определяме минималното съдържание на клетките, означени със знак - . В нашия случай то е 30. Това число се изважда от "минусовите" клетки и се прибавя към "плюсовите". Получаваме таблицата:

С нея постъпваме по аналогичен начин. Използвайки пълните клетки определяме потенциалите. Оценките за празните клетки са неотрицателни, което показва, че планът е оптимален.
Транспортните разходи са : 40.5+70.3+50.2+60.1+30.3+50.1=710.
• Задача 2 Начало

Намерете оптималните транспортни разходи за транспортната задача:


Решение:

Задачата е от отворен тип, поради това, че производството ( 30 + 20 = 50 ) е по-малко от потребностите ( 18 + 22 + 20 = 60 ). Поради това въвеждаме допълнителен производител с производство 10 единици с нулеви транспортни разходи. Таблицата придобива следния вид:




Попълваме на началния план по метода на минималните транспортни разходи.


За запълнените клетки определяме потенциалите така, че сумата им да бъде равна на транспортните разходи за всяка запълнена клетка. Тоест u_i + v_j = t_ij за всяка пълна клетка. За u₁ даваме произволна стойност, например 1. От пълната клетка (1,2) определяме v₂ = 0 а от (1,3) v₃ = 7. Предвижвайки се надолу, от клетка (2,3) определяме u₂ = -3 и т.н.

Определяме оценките D ij = ui + vj - tij за свободните клетки. D 11 = 1 + 5 - 3 = 3>0 ; D 22 = -3 + 0 - 5<0 ; D 32 = -5 + 0 - 0<0 ; D 33 = -5 + 7 - 0=2>0 ;




Две от клетките - (1,1) и (3,3) имат положителна оценка. Най голямата от тях е оценката за клетка (1,1). Тази клетка трябва да се запълни. Построяваме цикъл, започвайки от клетка (1,1) с ъглови клетки, които са запълнени и им поставяме знаци + и - .




Определяме минималното съдържание на клетките, означени със знак - . В нашия случай то е 8. Това число се изважда от "минусовите" клетки и се прибавя към "плюсовите". В случая ще получим две свободни клетки - (1,3) и (2,1). За да предотвратим израждането на плана, клетката с по малки транспортни разходи - (2,1) я оставяме със стойност 0 и я считаме за запълнена. Получаваме таблицата:




Отново определяме потенциалите ръководейки се само от запълнените клетки. На u1 даваме произволна стойност - напр. 1.




За наше общо съжаление, отново съществува клетка с положителна оценка. Това е клетката (3,3). Цикълът изглежда така:




Прибавяйки минималното съдържание от "минусовите" клетки ( 10 ) към "плюсовите" и изваждайки го от "минусовите" получаваме таблицата:


Използването на критерия на потенциалите ни убеждава в оптималността на последния план.
Транспортните разходи са: 8.3 + 22.1 + 10.2 + 10.4 + 10.0=106

Частни производни

• Задача 1 Начало

Намерете частните производни z'_x и z''_xx на:

Решение:


Екстремуми на функция две променливи

• Задача 1 Начало


Решение:

• Задача 2 Начало

Намерете локалните екстремуми на функцията:

Решение:


Интеграли

• Задача 1 Начало

Пресметнете интеграла:

Решение:

• Задача 2 Начало

Пресметнете интеграла:

Решение:

• Задача 3 Начало

Пресметнете интеграла:

Решение:


Вероятности

• Задача 1 Начало

Хвърлени са девет монети. Каква е вероятността на точно четири от тях лицевата страна да е отгоре?
Решение:
Използваме схемата на Бернули.

• Задача 2 Начало

Дискретна случайна величина X има закон на разпределението:

X	-1	0	2	4
P	0,2	0,2	0,3	0,3

Намерете стандартното отклонение на X.
Решение:

• Задача 3 Начало

Плътността на разпределение на случайна величина е:

Намерете a и дисперсията на X.
Решение:
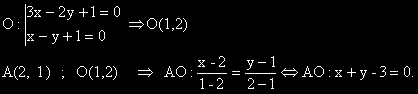