Какво трябва да знаем?
Тест на Ман-Уитни с ранжирани суми или U-тест
Да предположим, че имаме две непрекъснати и независими генерални съвкупности
X1 и X2 със средни стойности
μ1 и μ2 .
Условията за прилагане на теста са същите, както при този на Уилкоксън-Ман-Уитни или тест с ранжирани суми .
Нулевата хипотеза е равенството на средните на μ1 и μ2
от генералната съвкупност.
Нека обемите на двете извадки са n1 и n2 .
Наблюдаваните стойности на случайната величина се подреждат във възходящ ред като на всяка от тях се съпоставя пореден номер.
Ако има няколко повтарящи се стойности номерата, които им се съпоставят са едни и същи и са равни на средно-аритметичното
на поредните им номера, , както при този на Уилкоксън-Ман-Уитни или тест с ранжирани суми .
Да означим с N общия брой от двете извадки: N = n1 + n2 .
Нека R1 и R2 са сумите от номерата на наблюденията от първата и втората извадки.
В сила е равенството
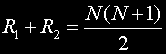
Помощните стойности U1 и U2 се изчисляват по формулите:
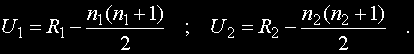
За U1 и U2 е в сила е равенството
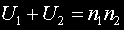
U - статистиката е по-малката от двете стойности:
U = min( U1, U2 ).
Тя се сравнява с критичната стойност
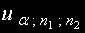 , зададена в таблиците при дадени n1 и n2 и зададена степен на значимост α.
, зададена в таблиците при дадени n1 и n2 и зададена степен на значимост α.
Ако алтернативната хипотеза е
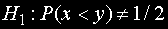 то при
то при
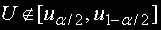 H0 се отхвърля.
Ако алтернативната хипотеза е
H0 се отхвърля.
Ако алтернативната хипотеза е
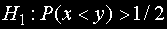 то при
то при
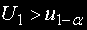 H0 се отхвърля.
Ако алтернативната хипотеза е
H0 се отхвърля.
Ако алтернативната хипотеза е
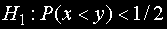 то при
то при
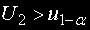 H0 се отхвърля.
H0 се отхвърля.
Пример
Данните са същите, както в примера за теста на ..Уилкоксън-Ман-Уитни или теста с ранжираните суми.
Там, ранжираните суми са R1 = 99 и R2 = 111.
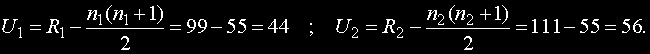 По-малкото от двете числа е 44 .
Изчислената статистика е U = 44.
При избраното ниво на значимост α = 0,05 и при обеми на извадките n1 и n2
определяме критичната стойност
По-малкото от двете числа е 44 .
Изчислената статистика е U = 44.
При избраното ниво на значимост α = 0,05 и при обеми на извадките n1 и n2
определяме критичната стойност
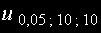 от таблицата .
Тя е
от таблицата .
Тя е
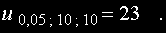 Понеже изчислената статистиката е по-голяма от критичната стойност
Понеже изчислената статистиката е по-голяма от критичната стойност
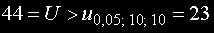 нулевата хипотеза не може да бъде отхвърлена.
нулевата хипотеза не може да бъде отхвърлена.
Прилагаме
таблици на критичните стойности на теста на Ман-Уитни с ранжирани суми или U-теста
При големи стойности на n1 >10 и n2 >10 разпределението на сл. вел U е
приблизително нормално със средна стойност n1 n2/2 и дисперсия
n1n2(N+1)/12.
В този пример може да се приложи и приближението с нормалното разпределение.
Какво ще научим: