Какво трябва да знаем?
Знаков тест на Уилкоксън или тест на ранжираните знаци
Знаковият тест не отчита големината на отклоненията а само знаците.
Тази неточност се поправя със знаковия тест на Вилкоксън.
При него отново се прави предположение за медианата,както при знаковия тест, но разпределението трябва да е симетрично.
Нека
{X1, X2, X3, ... , Xn}
е извадка от генералната съвкупност.
Изчисляват се абсолютните стойности на разликите
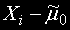и се подреждат в нарастващ ред като след тях се написват поредните им номера, но със знаците на разликите.
Нека W+ е сумата от поредните номера с положителен знак а
W- - сумата на тези с отрицателен.
Определя се минималната от двете стойности :
W = min( W+ , W- )
и от таблицата се определя критичната стойност
.
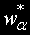Ако алтернативната хипотеза е
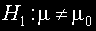и наблюдаваната стойност на статистиката w е по-малка от критичната, то нулевата хипотеза
се отхвърля и се приема алтернативната.
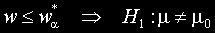
Пример:
За генералната съвкупност предполагаме че медианата е μ0 = 3,1.
Извадката е с обем 16 единици.
Намираме стойностите за всяка от тях Xi , разликите
Xi - μ 0 и абсолютните стойности на разликите
| Xi - μ 0 | :
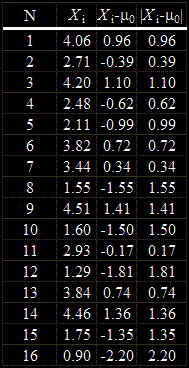Преподреждаме таблицата в нарастващ ред на последните и записваме поредните номера, снабдени със знаците на разликите:
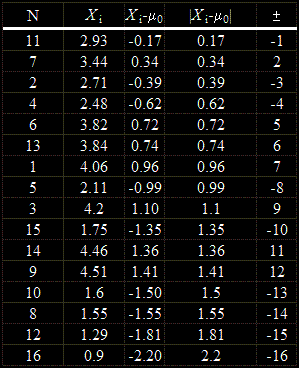Определяме W+ и W- :
W+ = 2+5+6+7+9+11+12=52.
W - = 1+3+4+8+10+13+14+15+16=84.
Минималната стойност на двете е w = 52.
От таблицата намираме
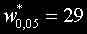при обем на извадката n=16 .
Понеже w=52 не е по-малко от критичната стойност, нулевата хипотеза не може да бъде отхвърлена.
Таблица на критичните стойности на знаковия тест на Вилкоксън
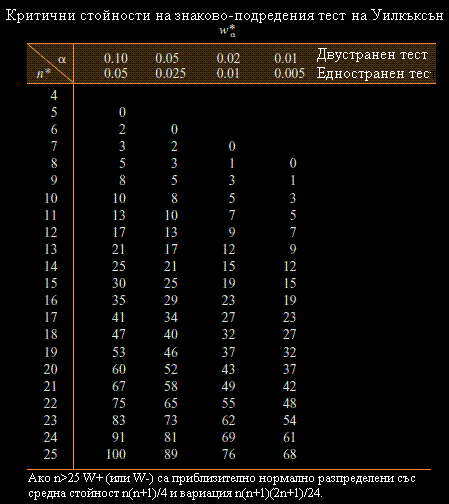
Какво ще научим: