Какво трябва да знаем?
Знаков тест
Знаковият тест се използва опровергаване на нулева хипотеза относно медианата на непрекъснато разпределение.
Медианата е тази стойност на случайната величина X, за която вероятността наблюдаваната стойност да е по-малка или равна на нея е 0,5.
Такава е и вероятността да е по-голяма:
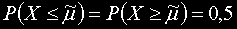
Нека
{X1, X2, X3, ... , Xn} е
случайна извадка от генералната съвкупност, чиято медиана искаме да оценим.
Определяме разликите
.
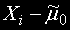Статистиката е броят на случаите, при които тези разлики са положителни.
Този брой ще означим с R+ .
Ако нулевата хипотеза е вярна, разликите с еднаква вероятност ще бъдат както положителни, така и отрицателни и R+ се подчинява на
Биномното разпределение b(n ; 0,5) .
Пример 1. Нека нулевата хипотеза и нейната алтернатива са:
.
Ще отхвърлим нулевата хипотеза в полза на алтернативната ако броят на положителните разлики е относително малък.
Нека r+ е определената статистика.
Ако изчислената P-стойност
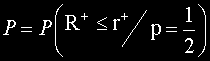е по-малка или равна на предварително зададено ниво на значимост α ще отхвърлим нулевата хипотеза .
Пример 2.
Желаем да преценим дали медианата на разпределението на случайната величина X от генералната съвкупност е 3,1 или е различна от тази стойност.
Извършваме извадка с обем 16, като получените стойностите са показани в следващата таблица:
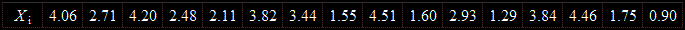Извършваме осемстъпкова проверка на хипотеза.
Оценявяният параметър е медианата на разпределението на случайната величина X на генералната съвкупност.
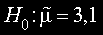Алтернативната хипотеза е
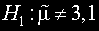Избираме ниво на значимост α = 0,05
Тестовата статистика е броят на положителните разлики в таблицата:
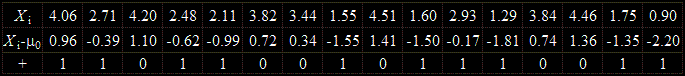R+ = 10
Ще отхвърлим нулевата хипотеза, ако P-стойността отговаряща на R+ = 10 е по-малка или равна на α = 0,05.
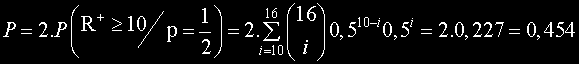Понеже P=0,454 не е по-малка от α = 0,05 не можем да отхвърлим нулевата хипотеза, че медианата на сл. вел. от генералнта съвкупност е равна на 3,1.
Изображение и пояснения:
?
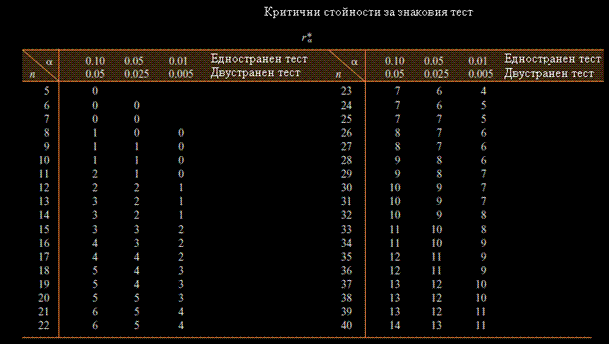
И най накрая таблицата на критичните стойности на знаковия тест, заимствана от [1]
Какво ще научим: