Условие за изпъкналост на функция

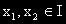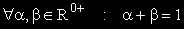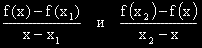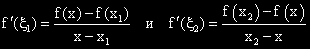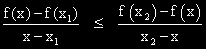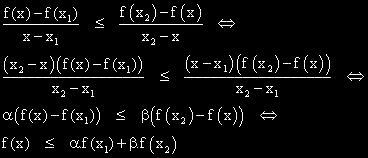
Какво трябва да знаем:
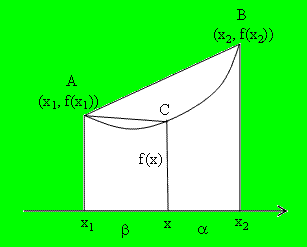
Неравенство на Йенсен
Изпъкналост на функция - дефиниция 		Изследване на функции


Теорема:
Диференцируемата функция y = f(x) е изпъкнала в интервала (а,в) = I тогава и само тогава,
когато производната 'и в този интервал е растяща функция.
Доказателство:
Необходимост ( Þ )
Нека f(x) е изпъкнала в интервала I=(a, b).

Трябва да докажем, че първата 'и производна е растяща.
Ясно е, че:
Неравенството може да се запише така:

Изваждайки f(x1 ) от двете страни на неравенството и използвайки, че 1 - a = b получаваме:
Понеже K е ъгловият коефициент на правата AB, това неравенство показва,
че отсечката AC има по малък ъглов коефициент от отсечката AB, или което е същото, че е под нея.


Нека сега да дадем възможност на x да се доближава към x1 .
Лявата част ще клони към f'(x1 ) а дясната е една константна величина, вече означихме с K.

Следващата ни цел е да покажем, че:

Отново изхождаме от неравенството:

Сега изваждаме f(x2 ) от двете страни на неравенството и използваме, че 1 - b = a. Получаваме:

Посоката на неравенството се променя, понеже x е по-малко от x2 .
Нека, сега, x да се доближава към x2 .
Лявата част ще клони към f'(x2 ) а дясната е константата K.

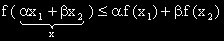
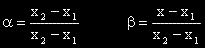
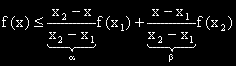
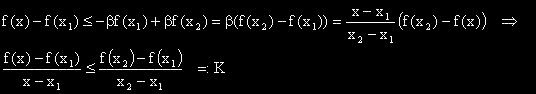
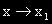
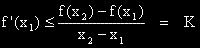
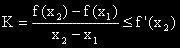
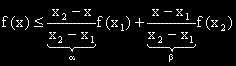
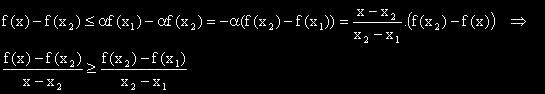
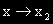
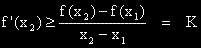
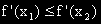Понеже K е между двете неличини f'(x1 ) и f'(x2 ) , получаваме: , което показва, че f'(x) е растяща функция.

Достатъчност ( Ü )
Нека f '(x) е растяща функция в интервала I = (a, b).
Трябва да докажем, че е изпълнено неравенството
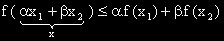, за всяко

и

Нека x Î (x1, x2)
Да разгледаме изразите:

Поради това, че f(x) е диференцируема функция съществуват числа x1 от (x1, x ) и x2 от (x, x2 ), такива, че:

От това, че f '(x) e растяща функция, следва, че:

Ще покажем, че това неравенство е еквивалентно на неравенството на Йенсен.
Умножаваме "на кръст" и делим на x2 - x1 .
Да забележим, че всички множители са положителни.



Нали така, другари!