Параметрично уравнение на права
Скаларно произведение на вектори
Интеграл
Контур
Затворена начупена, непресичаща се линия, образувана от поредица от точки в равнината и
свързващите ги отсечки ще наричаме контур.
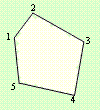
Този затворен контур е изпъкнал и се състои от 5 точки и толкова отсечки.
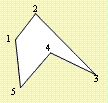
Този контур не е изпъкнал.
Параметрично зададени затворени криви
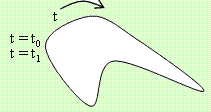
Нека x и y са функции от параметъра t, който се изменя от t0 до t1.
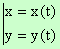
Предполагаме, че кривата е затворена: x(t0) = x(t1) и
y(t0) = y(t1) и е без самопресичане,
което се изразява с условието, че не съществуват двойка параметри t' и t" за които x(t') = x(t") и
y(t') = y(t").
За контура
При задаване на нашия контур използваме параметрично уравнение на всяка от съставяшите го отсечки.
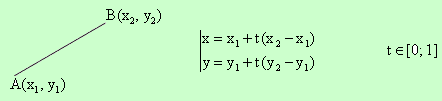
При t = 0 се получава точката A а при t = 1 - точката B.
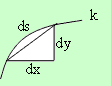
Елементарни дъги
Елементарната дължина на линията k, зададена със своите параметрични уравнениия, се определя от
равенството:
където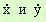 
са производните на x и y спрямо параметъра t.
Желаейки ds да бъде константа, ние можем да определим dt:
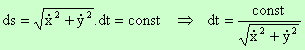
Чрез тази формула можем да определяме стъпката на параметъра - dt, така, че елементарната дължина
да бъде простоянна.
Освен това, на всяка елементарна дъга ds от контура k конструираме вектор, отговарящ на следните условия:
1. Той е перпендикулярен на допирателната в средната точка на дъгата ds.
2. Насочен е навън от контура k.
3. Дължината му е равна на дължината на елементарната дъга ds.
Този вектор ще означаваме с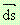 
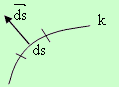
Ако на всяка елементарна дъга от контура k се съпостави описания вектор се получава
нещо като "таралеж".
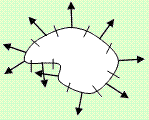
Предполагаме, че дължините на елементарните дъги са едни и същи,
следователно и бодлите на таралежа са еднакво дълги.
Колкото е по-прецизно разделянето на контура, т.е. колкото повече и по-къси са дъгите,
толкова повече са векторите, но за сметка на това са по-къси.
Векторно поле
Нека на всяка точка A от равнината е съпоставен вектор
.
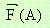Точката, както и вектора се задават със своите координати
.
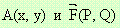Координатите на вектора F зависят от x и y.
Така, че: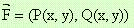 
.
Векторните полета се изобразяват в една ограничена област в равнината с разумна гъстота.
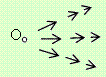Едно векторно поле се нарича централно, ако векторът
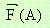е колинеарен на 
,
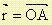където O е началото на координатната система.
Електростатичното поле, например, създадено от точков заряд в точката O има вида
Силата на отблъскване
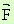има дължина
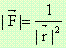и тя (силата) е колинеарна на
.
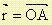Поток на векторно поле по затворен контур
Нека е зададен контурът k, разделен на елементарни дъги и съответстващия му "таралеж".
Векторите на последния ще означаваме с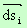 
и на чертежа те са изобразени с черен цвят.
Нека е зададено оше и едно централно векторно поле ,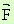
- червените вектори.
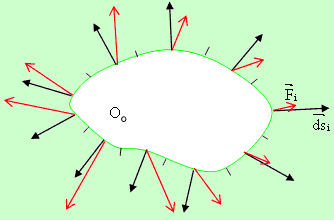Да умножим скаларно векторите
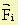и 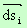и съберем тези произведения.
Разделяйки контура все по-прецизно, ние ще се доближим до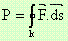 
Кръгчето в интеграла показва, че интегрирането се извършва в затворен контур.
Ако си представим векторното поле като преместване на материя по посока на съответния му вектор,
то P има физически смисъл на преминаващата през контура материя.
Ако P е положително то от контура k излиза материя, а ако е отрицателно k привлича материя.
Да разгледаме един пример.
Нека е зададено централно поле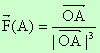 
и контур, състоящ се от две кончентрични, четвърт - окръжности с радиуси r и R и отсечки по осите,
като е показано на чертежа.
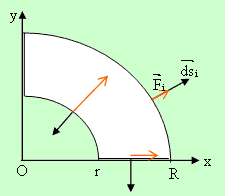
По голямата окръжност дължината на вектор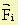а е 1 / R2
а на 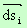е R.dt.
Понеже двата вектора са еднопосочни, интегралът по голямата дъга е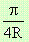 
.
Аналогично по малката дъга той е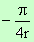 
.
По двете отсечки потокът е нула поради перпендикулярността на векторите.
Окончателно потокът е отрицателен.
Дали той е такъв за всяко централно поле с източник извън контура.
Програмния експеримент показва че е така.
Да бъдем програмисти!.
Алгоритъм за това, дали една точка е вътрешна за един затворен контур
Ние, като нормални хора, ще кажем:
" Какъв е смисълът да правим програма, като това се вижда с просто око."
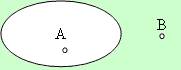
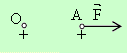
A е вътрещна а B - външна
Но за по-сложни контури това не е съвсем очевидно.
Например за този.
Или за този, взет от книгата на Р. Курант и Г. Робинс "Що е математика"
Математикът Жордан е казал, че всеки затворен, непресичащ се контур разделя равнината на две части -
вътрешна и външна.
Ако две точки са от една и съща част, те могат да бъдат свързани с линия, непресичаща контура.
Теоремата е била доказана много трудно, въпреки своята очевидност.
Можем да си мислим и така:
Една точка A е вътрешна за контура, ако произволен лъч с начало точката A пресича контура в нечетен
брой точки и външна в противоположния случай.
Точката е вътрешна, защото лъчът пресича контура в 3 точки.
Възникват усложнения, ако лъчът има обща отсечка с контура.
Тук ще постъпим по следния начин:
1. Разделяме контура на малки участъци с равни дължини.
Участъците ще ги считаме за отсечки.
2. Построяваме вектор за всеки участък, перпендикулярен на кривата и насочен навън спрямо контура.
3. Конструираме централно поле спрямо изследваната точка и определяме потока му спрямо контура.
Ако той е положителен - точката е вътрешна, ако не - външна.
За работата с програмата
Контура се чертае по обичайния начин с мишката, отляво надясно,
като eдновременно с последната отсечка трябва да се натисне клавиша "Shift".
От избора - наречен "File" избираме "Drow" за да видим затворения контур.
Щракаме с мишката в произволна точка.
Ако точката е върешна, в полето на радактора се появява надписът "In" иначе - "Out" .
Работи ли? Работи. К'о поичи искате от мен.
За програмата
Тя се състои от няколко части (Unit).
За векторите
В частта за векторите основните подпрограми са:
function DotProdR(A,B:TVectR):real; Скаларно произведение
function RotLeft90R(A:TVectR):TVectR; Завъртане на вектора наляво на 90 градуса
function VectFieldCntrlR(Point,IniPoint:TVectR):TVectR; Създава на централно векторно поле в точката "Point" с начална точка "IniPoint"
procedure LenghtR(var A:TVectR); Изчислява дължината на вектора
procedure NormingR(var A:TVectR); Нормира го (разделя го на дължината му ).
В резултат се получава единичен вектор.
procedure PrNumbR(r:real;var A:TVectR); Умножава вектора по число.
За контура
В частта за контура (StClasses - най трудната) са разположени програмите,
отговарящи за информацията за върховете на контура, необходима за неговото изобразяване и програмата
за определяне на това, дали една точка е вътрешна или външна за него -
function InOut(X,Y:integer):boolean;.
Ще се спрем на тази програма.
Читателите, които се интересуват от програмния клас трябва да обърнат внимание на
създателите и унищожителите на класове.
Тук няма да ги коментираме.
X,Y са координатите на точката, за която се определя дали е вътрешна или не.
const ds=10 е фиксираната дължина на една елементарна дъга.
End_j -Броят на елементарните дъги в една отсечка от контура.
Sum Тук се натрупва потокът на векторното поле.
ABR е един помощен вектор, който в началото представлява векторът по една насочена отсечка по контура.
После той се нормира и завърта.
dSigma - векторът, представляващ - бодил от таралежа.
За една отсечка от контура той е постоянен, перпендикулярен на отсечката и насочен навън от контура.
ItemO и ItemN са върховете на една отсечка от контура.
Чрез проверката:
if(i < Vertices.Count) then ItemN:=Vertices.Items[i]
се осигурява последната отсечка да бъде затварящата контура.
Информацията от върховете на контура ItemO и ItemN се използва за определянето на вектора ABR.
Дължината на текущата отсечка се разделя на части с еднакви дължини - равни на тази на .
Броят им е End_j.
За средата на всяка една от тези малки отсечки се определя векторното поле
vField и потока през нея.
Натрупва се в Sum.
И така нататък за вътрешния цикъл, движещ се по една единствена отсечка от контура.
И така нататък за външния, обхождащ всичките негови отсечки, включително и затварящата.
Работи ли? Работи. К'о поичи искате от мен.
Можете да изтеглите ZIP-версия на програмата: